Аэродинамику твердого тела, движущегося в жидкости, обычно рассматривают в одной из двух систем координат: скоростной или связанной.
Продольная ось 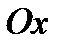 скоростной системы направлена всегда по вектору скорости движения центра масс аппарата, вертикальная ось
скоростной системы направлена всегда по вектору скорости движения центра масс аппарата, вертикальная ось 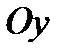 расположена в вертикальной плоскости симметрии тела и направлена вверх, ось
расположена в вертикальной плоскости симметрии тела и направлена вверх, ось 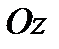 направлена так, чтобы образовывать с осями
направлена так, чтобы образовывать с осями 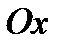 и
и 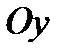 правую тройку (рис.2.9а), [7,10].
правую тройку (рис.2.9а), [7,10].
Аэродинамические расчеты могут вестись также в связанной системе координат. Обычно именно в этой системе исследуется вращательное движение тела. В этой системе, жестко связанной с летательным аппаратом, ось 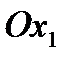 направлена вдоль главной продольной оси инерции, вертикальная ось
направлена вдоль главной продольной оси инерции, вертикальная ось 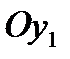 расположена в вертикальной плоскости симметрии, горизонтальная ось
расположена в вертикальной плоскости симметрии, горизонтальная ось 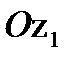 направлена так, чтобы с осями
направлена так, чтобы с осями 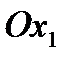 и
и 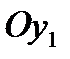 образовывать правую тройку (рис.2.9б).
образовывать правую тройку (рис.2.9б).
Рис.2.9 – Силы и моменты в скоростной (а) и связанной (б) системах координат
Проекции вектора 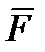 на оси скоростной системы координат называются соответственно силой лобового сопротивления
на оси скоростной системы координат называются соответственно силой лобового сопротивления 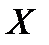 , подъемной силой
, подъемной силой 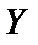 и боковой силой
и боковой силой 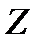 . Соответствующие проекции того же вектора на оси связанной системы координат называются продольной (осевой) (
. Соответствующие проекции того же вектора на оси связанной системы координат называются продольной (осевой) (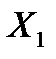 или
или 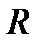 ), нормальной (
), нормальной (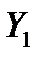 или
или 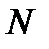 ) и поперечной
) и поперечной 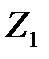 силами.
силами.
Проекции вектора 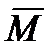 в той и другой системах координат имеют одно и то же название, а именно: составляющие относительно продольной оси называются моментом крена (соответствующие обозначения в скоростной системе
в той и другой системах координат имеют одно и то же название, а именно: составляющие относительно продольной оси называются моментом крена (соответствующие обозначения в скоростной системе 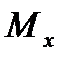 , в связанной -
, в связанной - 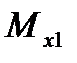 ), составляющие относительно вертикальной оси – моментом рыскания (
), составляющие относительно вертикальной оси – моментом рыскания (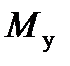 ,
, 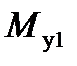 ), составляющие относительно поперечной оси – моментом тангажа (
), составляющие относительно поперечной оси – моментом тангажа (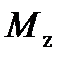 ,
, 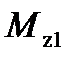 ).
).
Таким образом, можем записать:
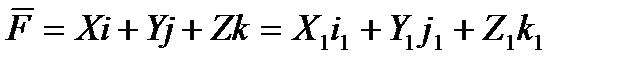 ;
;
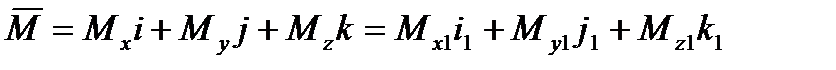 ,
,
где 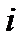 ,
, 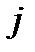 ,
, 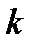
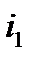 ,
, 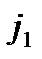 ,
, 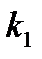 - единичные векторы по осям соответственно скоростной и связанной систем координат. Положительным моментом относительно оси считается момент, который стремится повернуть летательный аппарат против часовой стрелки, если вести наблюдение за движением вектора с его конца.
- единичные векторы по осям соответственно скоростной и связанной систем координат. Положительным моментом относительно оси считается момент, который стремится повернуть летательный аппарат против часовой стрелки, если вести наблюдение за движением вектора с его конца.
Величина и направление действия сил и моментов зависят при данной скорости полета на некоторой высоте от ориентировки тела относительно вектора своей скорости 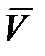 . В свою очередь эта ориентировка обуславливает соответствующее взаимное расположение связанной и скоростной систем координат. Такое расположение определяется двумя углами:
. В свою очередь эта ориентировка обуславливает соответствующее взаимное расположение связанной и скоростной систем координат. Такое расположение определяется двумя углами: 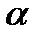 - углом атаки,
- углом атаки, 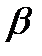 - углом скольжения. На рис.2.10 показано, как положение дирижабля, корпус которого имеет плоскость симметрии, характеризуется в скоростной системе координат углами
- углом скольжения. На рис.2.10 показано, как положение дирижабля, корпус которого имеет плоскость симметрии, характеризуется в скоростной системе координат углами 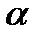 и
и 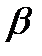 .
.
Первый из них (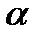 ) есть угол между осью
) есть угол между осью 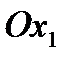 и проекцией вектора скорости
и проекцией вектора скорости 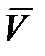 на плоскость продольной симметрии
на плоскость продольной симметрии 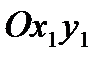 (на рис.2.10 – плоскость
(на рис.2.10 – плоскость 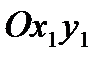 обозначена
обозначена  , а указанная проекция - вектор
, а указанная проекция - вектор 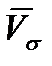 ), второй (
), второй (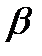 ) представляет собой угол между вектором
) представляет собой угол между вектором 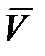 и плоскостью
и плоскостью 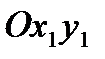 (т.е. между
(т.е. между 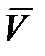 и
и 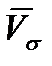 ).
).
Рис.2.10 – К определению углов атаки 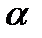 и скольжения
и скольжения 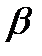 ;
; 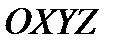 - скоростная система координат; плоскость
- скоростная система координат; плоскость 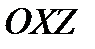 перпендикулярна плоскости симметрии тела.
перпендикулярна плоскости симметрии тела.
Зная углы атаки и скольжения, можно перейти от проекций векторов силы и момента в одной системе координат к проекциям этих векторов в другой системе координат. Формулы пересчета, которые легко получаются по рис.2.10, имеют вид:
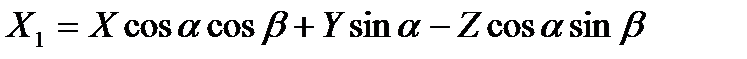 ,
,
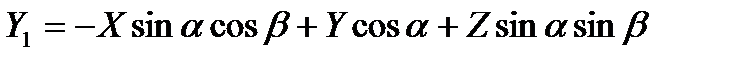 ,
,
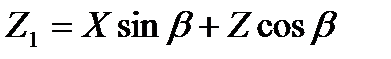 , (2.58)
, (2.58)
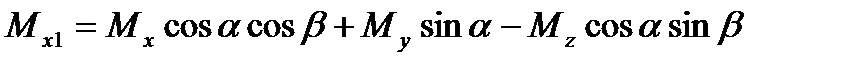 ,
,
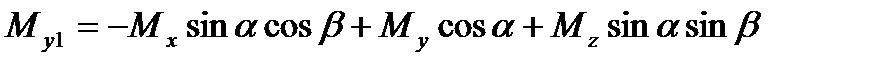 ,
,
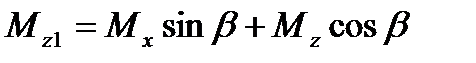 . (2.59)
. (2.59)
 2015-01-21
2015-01-21 984
984








