Ускоренное движение. Матрица присоединенных масс

Случай ускоренного движения дирижабля встречается при анализе его движения на этапах торможения и разгона. Кроме того, тело приобретает дополнительное ускорение также под воздействием воздушных порывов. Особенность дирижаблей состоит в том, что в этом случае большую роль играют инерционные свойства окружающей среды, тогда как при рассмотрении других летательных аппаратов, например, самолетов, ими обычно можно пренебречь [11,12].

При малых скоростях движения в нижних слоях атмосферы воздушную среду можно считать несжимаемой идеальной жидкостью. Напомним, что идеальность означает отсутствие трения между слоями жидкости а также отсутствие касательных напряжений на поверхности движущегося в такой жидкости твердого тела.

Итак, рассмотрим общий случай неравномерного и непоступательного движения твердого тела сквозь несжимаемую идеальную жидкость, предполагая, что центр тяжести тела движется с данным ускорением, а само тело заданным образом вращается вокруг мгновенной оси, проходящей через центр тяжести.

Будем использовать две системы координат: неподвижную, инерциальную 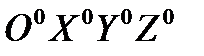, и движущуюся вместе с телом - 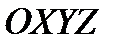, начало которой совмещено с центром масс тела.

Считая движение жидкости вокруг тела безвихревым, используя условия несжимаемости жидкости и непротекания поверхности, можно получить [9], что потенциал скоростей возмущения жидкости удовлетворяет уравнению Лапласа 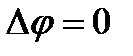и представляет собой линейную комбинацию

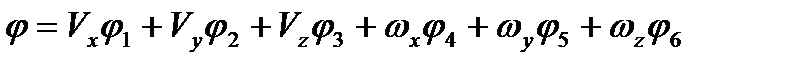(2.63)

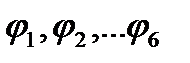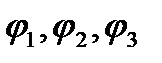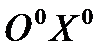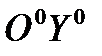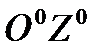элементарных потенциалов , смысл которых следующий. Функции в каждый данный момент представляют потенциалы скоростей того возмущенного движения жидкости, которое возникает при поступательном движении данного тела с единичной скоростью, параллельной, соответственно, осям , и ; функции 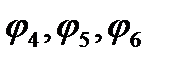аналогично представляют потенциалы возмущений от чисто вращательных движений тела с единичными угловыми скоростями вокруг осей 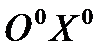, 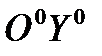и . 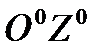Функции 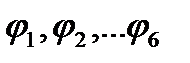предполагаются гармоническими, т.е. удовлетворяющими уравнению Лапласа, стремящимися к нулю при удалении от тела и удовлетворяющими в каждый момент времени следующим граничным условиям на его поверхности:

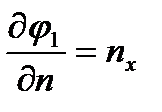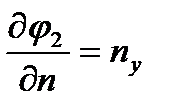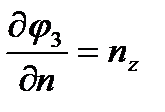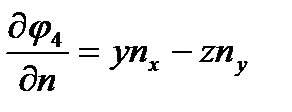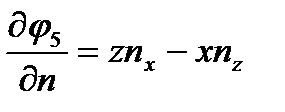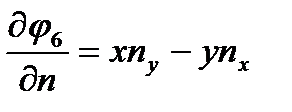, , , , , .(2.64)

Каждая из этих функций по отдельности может быть найдена известными методами ([9]). Будем вычислять частичные потенциалы 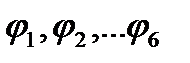в связанной системе 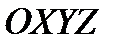. Тогда, в силу независимости проекций нормали в каждой точке поверхности тела от времени, потенциалы 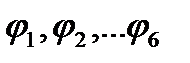также не зависят от .

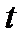Можно показать, что уравнения динамики твердого тела, движущегося в жидкости, обладающей указанными свойствами (идеальной и несжимаемой), в инерциальной системе 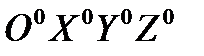имеют вид:

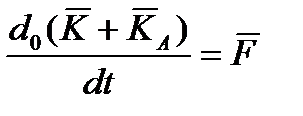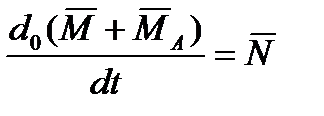, , (2.65)

где индекс “0” при дифференциале означает, что рассматривается производная данной величины в инерциальной системе координат (так как приращения одного и того же вектора в инерциальной и неинерциальной системах отсчета в общем случае различны); 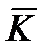и 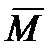- собственные векторы количества движения и момента количества движения тела в пространстве без жидкости под действием векторов внешних силы и момента сил 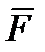, , 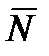в которые не входят силы и моменты реакции жидкост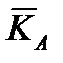и; и 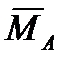- так называемые “присоединенные” количество движения и момент количества движения, обусловленные влиянием сплошной среды, в которой движется тело. При этом векторы 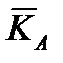и 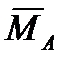выражаются в виде следующих интегралов по поверхности тела от функций, зависящих от частичных потенциалов:

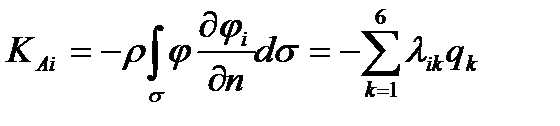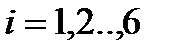, , (2.66)

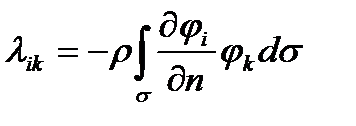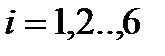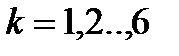, , , (2.67)

где 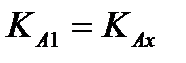, , 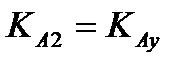, , 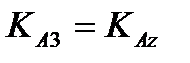, , 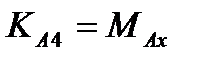, , 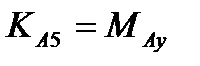, , 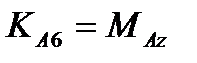, 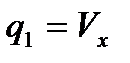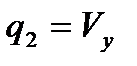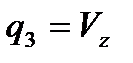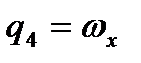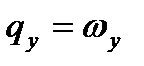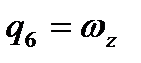; 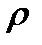- плотность среды.

Являясь коэффициентами в выражении “присоединенных” количества и момента количества движения через обобщенные скорости 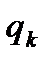, величины 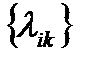играют роль инерционных коэффициентов, “присоединяющихся” к инерционным коэффициентам, входящим в аналогичные выражения количества движения и момента количества движения самого твердого тела.

Поэтому величины 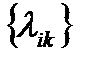называются присоединенными массами.

В неинерциальной системе отсчета 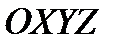уравнения динамики твердого тела, движущегося в несжимаемой идеальной жидкости, согласно (2.10) и (2.15)-(2.18) имеют вид [4]:

,

.

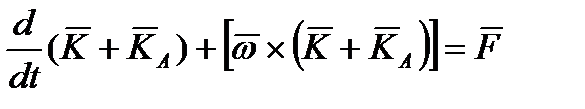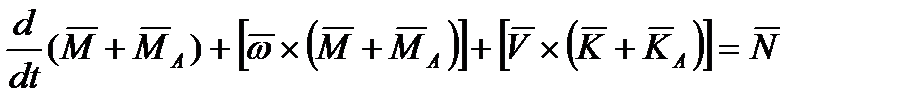Эти равенства перепишем в виде:

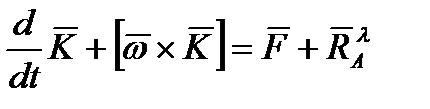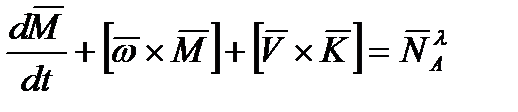, , (2.68)

где

, .

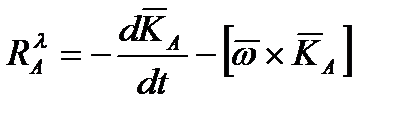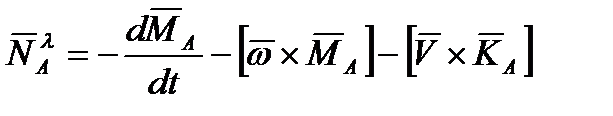Использование равенства (2.68) на основании (2.66) позволяет получить формулы для проекций аэродинамических силы 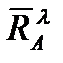и момента 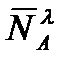за счет инертных свойств среды в связанной системе координат:

, ,

, ,

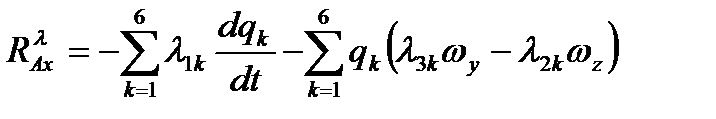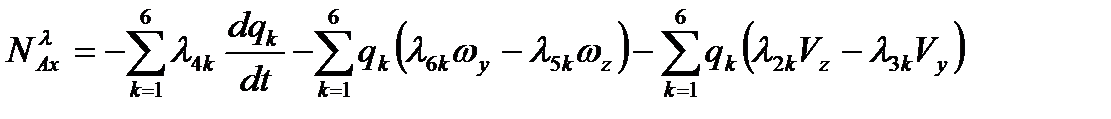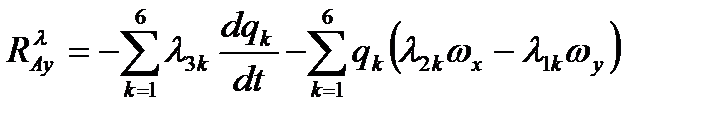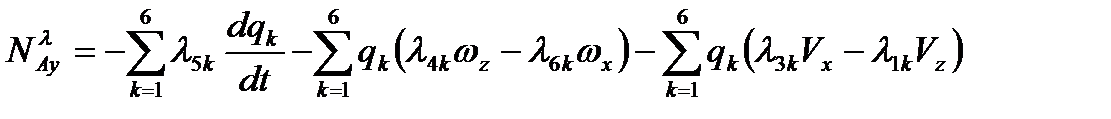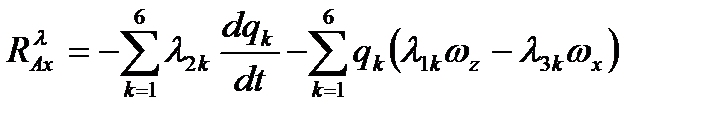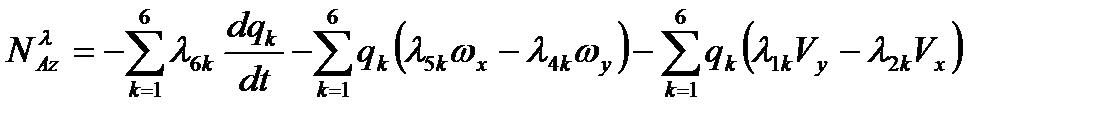, . (2.69)

Проекции (2.69) входят в правые части равенств (2.31)-(2.36).

В качестве примера рассмотрим влияние сплошной среды на тело вращения, движущееся с ускорением.

В первом приближении считаем, что тело движется так, что всеми присоединенными массами кроме 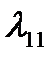, , 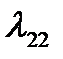, 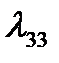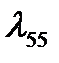и 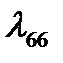можно пренебречь.

Тогда уравнения ускоренного движения тела вдоль осе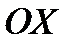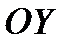й , и 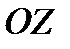в некоторой инерциальной системе координат имеют вид [12]:

, , ,

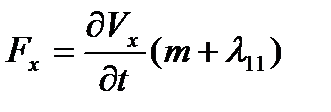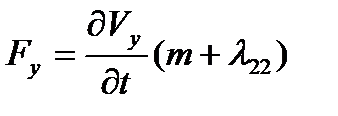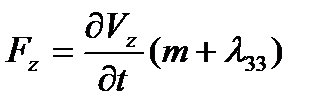где 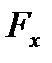, , 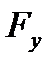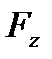проекции силы, которую необходимо приложить к телу, чтобы оно получило ускорение с компонентами 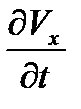, , 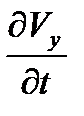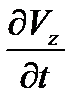в данной сплошной среде; 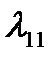, , 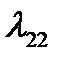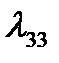определяются по формуле (2.67). Заметим, что в силу симметрии тела относительно оси 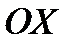выполняется равенство .

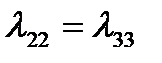На практике обычно пользуются так называемыми коэффициентами присоединенных масс 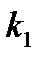, , 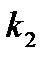, 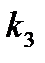которые следующим образом связаны с 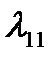, 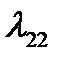и :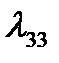

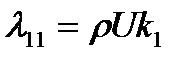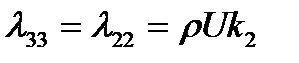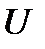, , ( - объем тела). (2.70)

Потенциалы 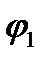, , 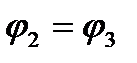фигурирующие в формуле (2.66), и которые необходимо знать для последующего определения 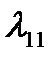, , 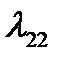, 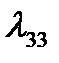находятся по потенциалам продольного и поперечного обтеканий тела вращения за вычетом соответствующих значений потенциалов невозмущенных потоков [9,12].

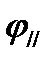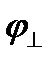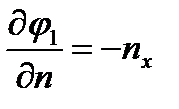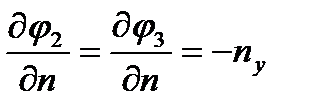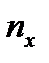Используя условие непротекания для потенциалов и , можно показать, что , , где и 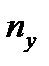- проекции единичной нормали к поверхности тела в данной ее точке. Поэтому , .

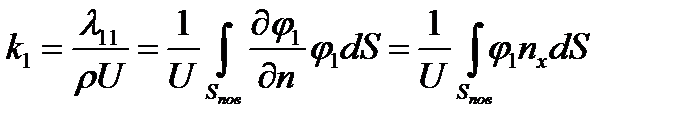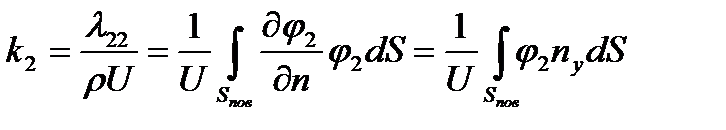Аналогично рассматривается случай вращения корпуса дирижабля с угловым ускорением 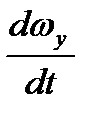вокруг ос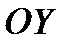и или 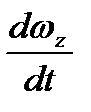вокруг оси 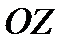, проходящих через центр объема . В этом случае уравнение вращательного момента в инерциальной системе отсчета определяется второй формулой в (2.84), которая в случае каждого из указанных вращений в инерциальной системе координат примет вид:

, ,

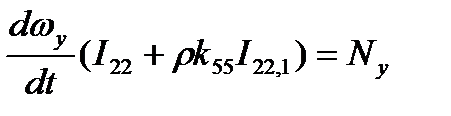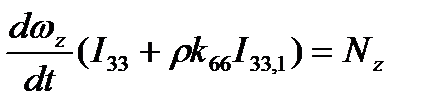где

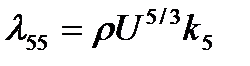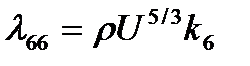, , (2.71)

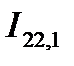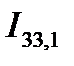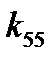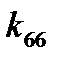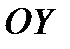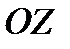и - соответствующие осевые моменты инерции однородного тела единичной плотности в связанной с дирижаблем системе, причем это тело совпадает по форме и размерам с корпусом дирижабля; и коэффициенты присоединенных моментов инерции по осям и соответственно.

В приближенных аэродинамических расчетах корпус дирижабля заменяется эллипсоидом вращения с удлинением 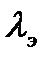, совпадающим с удлинением дирижабля 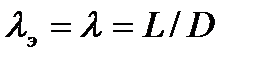. В этом случае рассмотренные коэффициенты присоединенных масс рассчитываются по выражениям [9,12]:

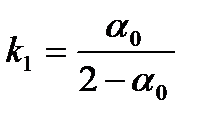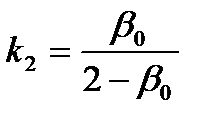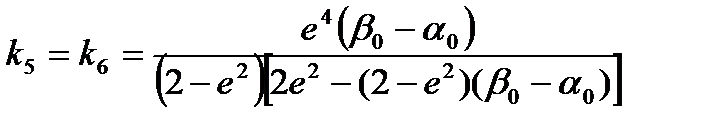, , , (2.72)

где 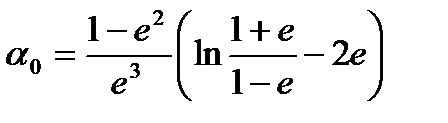, , 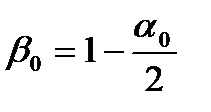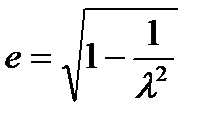-эксцентриситет эллипсоида