Покажем, что аэродинамическое свойства твердого тела при его равномерном поступательном движении в сплошной среде могут быть охарактеризованы пятью безразмерными коэффициентами, называемыми аэродинамическими.
Ранее было указано, что на каждую элементарную площадку 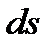 на поверхности обтекаемого тела действует некоторая условно сосредоточенная сила
на поверхности обтекаемого тела действует некоторая условно сосредоточенная сила 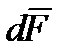 . Поскольку сила
. Поскольку сила 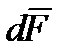 , действует на некоторую элементарную поверхность, она называется также поверхностной силой.
, действует на некоторую элементарную поверхность, она называется также поверхностной силой.
Рассмотрим следующую задачу. Пусть при некоторых углах атаки и скольжения, а также заданных параметрах набегающего потока (скорость 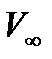 , статическое давление
, статическое давление 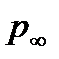 , плотность
, плотность 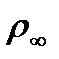 и температура
и температура 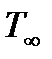 ) известно распределение по поверхности обтекаемого тела давления
) известно распределение по поверхности обтекаемого тела давления 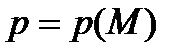 и касательного напряжения
и касательного напряжения 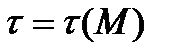 . Требуется определить суммарные значения аэродинамических сил и моментов, действующих на тело.
. Требуется определить суммарные значения аэродинамических сил и моментов, действующих на тело.
На выделенную площадку 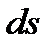 действуют нормальная сила величиной
действуют нормальная сила величиной 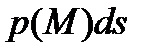 и касательная сила величиной
и касательная сила величиной 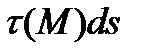 . Однако можно показать, что воздействие жидкости на тело эквивалентно суммарному воздействию всех сил от избыточного давления
. Однако можно показать, что воздействие жидкости на тело эквивалентно суммарному воздействию всех сил от избыточного давления 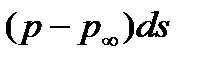 (это давление
(это давление 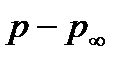 называется аэродинамическим) и сил касательных напряжений
называется аэродинамическим) и сил касательных напряжений 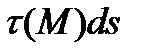 , распределенных по поверхности тела. Поэтому, проектируя векторы избыточного давления
, распределенных по поверхности тела. Поэтому, проектируя векторы избыточного давления 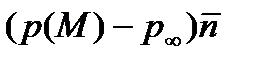 и касательного напряжения
и касательного напряжения 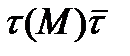 на оси координат скоростной системы, получим [10]:
на оси координат скоростной системы, получим [10]:
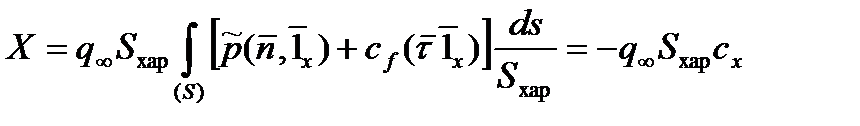 ,
,
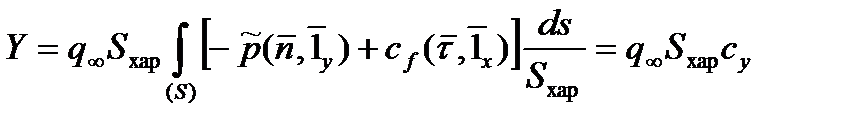 ,
,
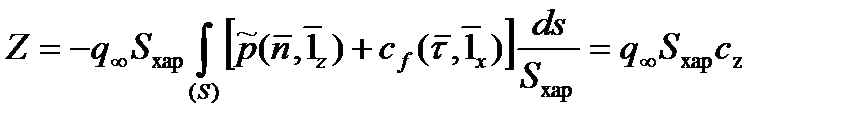 , (2.60)
, (2.60)
где 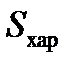 - характерная площадь тела,
- характерная площадь тела, 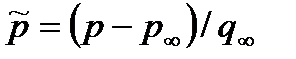 ,
, 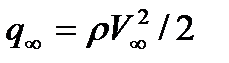 ,
, 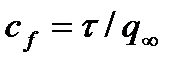 , безразмерные величины
, безразмерные величины 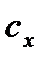 ,
, 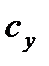 и
и 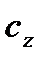 называются соответственно аэродинамическими коэффициентом силы лобового сопротивления, коэффициентом подъемной силы и коэффициентом боковой силы.
называются соответственно аэродинамическими коэффициентом силы лобового сопротивления, коэффициентом подъемной силы и коэффициентом боковой силы.
В качестве характерной площади тела могут быть выбраны, например, площадь миделева сечения тела (сечения, перпендикулярного продольной оси тела и максимальной площади) или величина 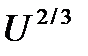 , где
, где 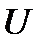 - объем тела.
- объем тела.
Аналогично получаются выражения для моментов через соответствующие безразмерные коэффициенты. А именно, для момента тангажа 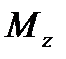 , момента рыскания
, момента рыскания 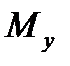 и момента крена
и момента крена 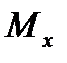 справедливы следующие интегральные представления:
справедливы следующие интегральные представления:
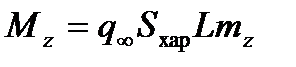 ,
, 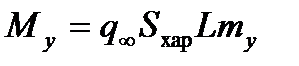 ,
, 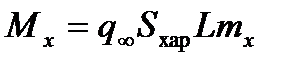 ,
,
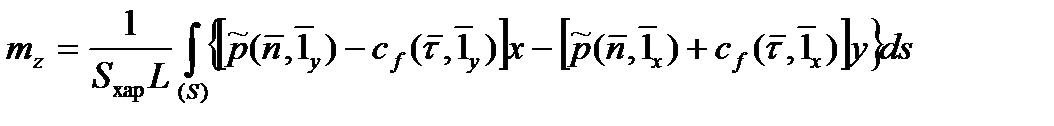 ,
,
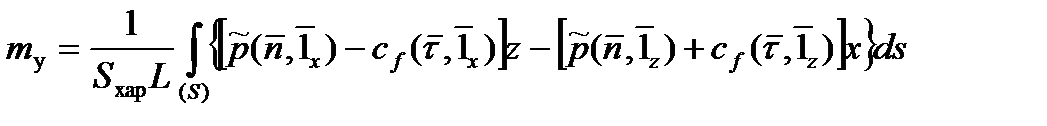 ,
,
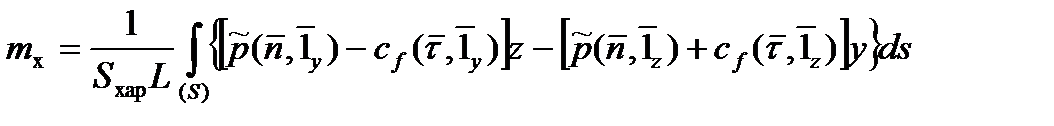 , (2.61)
, (2.61)
где 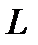 - некоторый характерный геометрический размер, например, максимальная длина тела; выражения
- некоторый характерный геометрический размер, например, максимальная длина тела; выражения 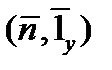 ,
, 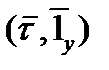 и т.д. - скалярные произведения соответствующих единичных векторов – имеют смысл направляющих косинусов между соответствующими направлениями.
и т.д. - скалярные произведения соответствующих единичных векторов – имеют смысл направляющих косинусов между соответствующими направлениями.
В связанной системе координат рассматривают аэродинамические коэффициенты продольной, нормальной и поперечной сил (соответственно, 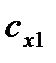 ,
, 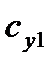 и
и 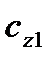 ) а также моменты крена, рыскания и тангажа в связанной системе координат (
) а также моменты крена, рыскания и тангажа в связанной системе координат (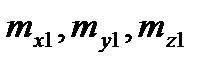 ). При помощи этих коэффициентов силы и моменты, действующие в этой системе, можно представить в следующем виде:
). При помощи этих коэффициентов силы и моменты, действующие в этой системе, можно представить в следующем виде:
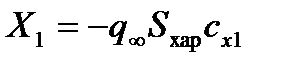 ,
, 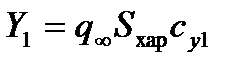 ,
, 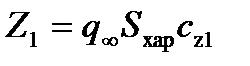 ,
,
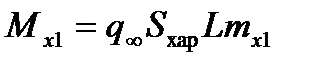 ,
, 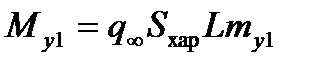 ,
, 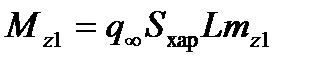 . (2.62)
. (2.62)
Для перехода от 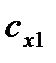 ,
, 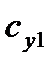 ,
, 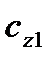 ,
, 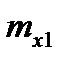 ,
, 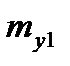 ,
, 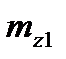 к
к 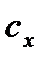 ,
, 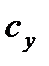 ,
, 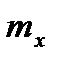 ,
, 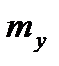 и
и 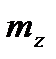 используются формулы связи, аналогичные выражениям (2.58) и (2.59).
используются формулы связи, аналогичные выражениям (2.58) и (2.59).
 2015-01-21
2015-01-21 1592
1592








