Вязко-упругое тело Максвелла

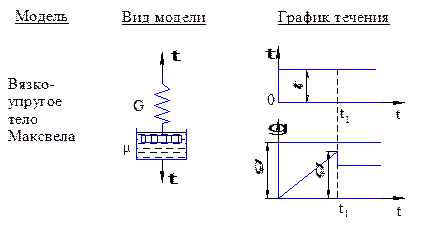
При приложении мгновенного напряжения система мгновенно деформируется как упругое тело на какую-то величину.

После мгновенной упругой деформации продолжается вязкое течение. Если к телу Максвелла приложить напряжение и по достижении им некоторой деформации зафиксировать эту деформацию, то со временем приложенное напряжение будет уменьшаться и исчезнет.

Явление самопроизвольного уменьшения напряжений при постоянной деформации называется релаксацией напряжений.

Уравнение тела Максвелла имеет вид:

,

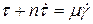где n – коэффициент, выраженный в секундах, называемый коэффициентом времени релаксации.

После математической обработки уравнение, характеризующее явление релаксации, имеет вид

.

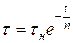График этого уравнения будет иметь следующий характер

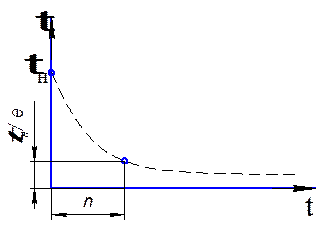Из графика видно, что коэффициент времени релаксации, равный промежутку времени, в течении которого начальное напряжение уменьшается в 2,7 раз, определяется по характеру кривой.