1. Амплитуда затухающих колебаний за время t 1 = 5 мин уменьшилась в 2 раза. За какое время t 2, считая от начального момента, амплитуда уменьшится в 8 раз?
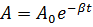
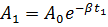
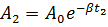
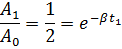
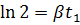
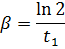
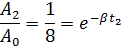
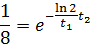
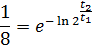
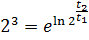
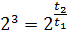
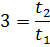
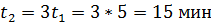
Ответ: 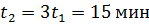 .
.
2. За время t = 8 мин амплитуда затухающих колебаний маятника уменьшилась в 3 раза. Определить коэффициент затухания.
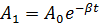
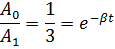
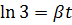
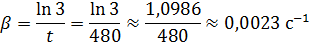
Ответ: 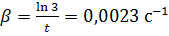 .
.
3. Амплитуда колебаний маятника длиной l = 1 м за время t 1 = 5 мин уменьшилась в 2 раза. Найти логарифмический декремент колебаний λ.
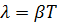
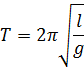
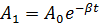
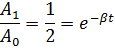
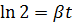
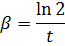
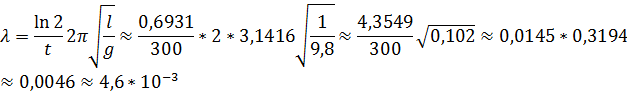
Ответ: 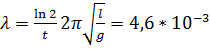 .
.
4. Пружинный маятник (жёсткость пружины k, масса груза m) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r. Определить коэффициент затухания β и резонансную амплитуду Aрез, если амплитудное значение вынуждающей силы F 0.
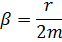
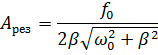
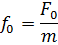
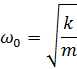
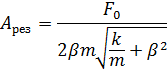
Ответ: 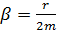 ;
; 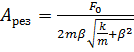 .
.
5. Определить период T затухающих колебаний, если период T 0 собственных колебаний системы равен 1 сек и логарифмический декремент колебаний λ = 0,628.
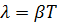
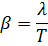
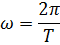
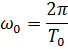
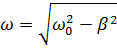
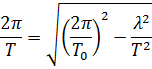
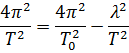
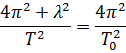
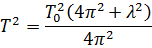
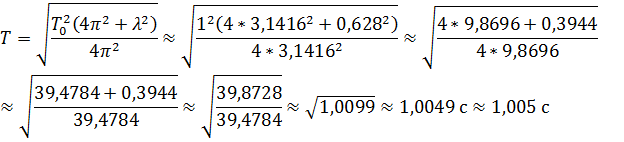
Ответ: 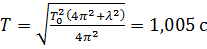 .
.
6. Определить, на сколько резонансная частота отличается от частоты ν 0 = 1 кГц собственных колебаний системы, характеризуемой коэффициентом затухания β = 400 с-1.
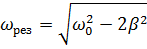
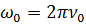
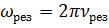
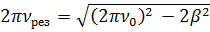
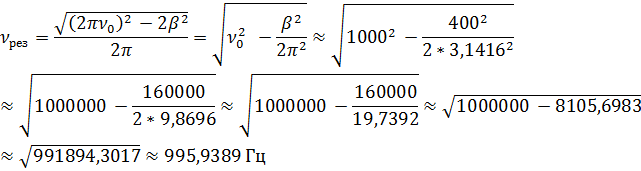
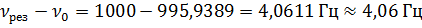
Ответ: 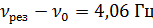 .
.
7. Колебательная система совершает затухающие колебания с частотой ν = 1000 Гц. Определить частоту ν 0 собственных колебаний, если резонансная частота ν рез = 998 Гц.
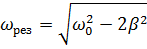
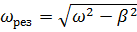
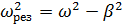
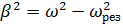
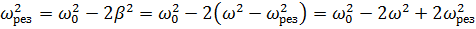
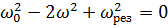
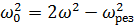
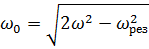
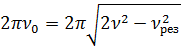
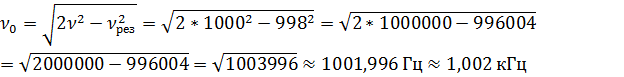
Ответ: 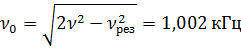 .
.
8. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания λ 0 = 1,5. Каким будет значение λ, если сопротивление среды увеличить в n = 2 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны?
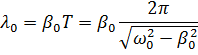
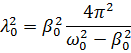
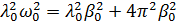
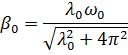
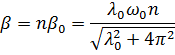
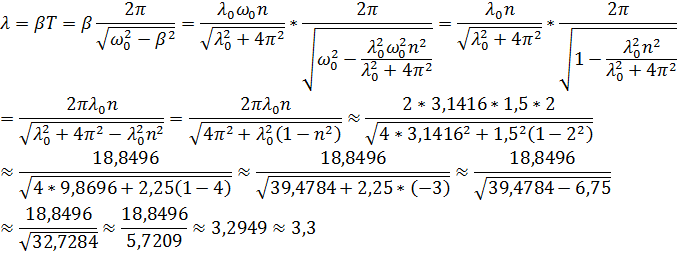
Колебания невозможны при 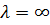 , то есть:
, то есть: 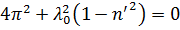
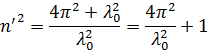
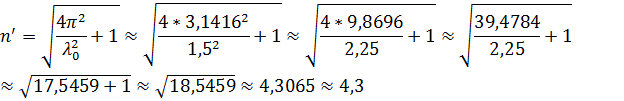
Ответ: 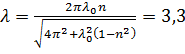 ;
; 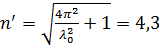 .
.
Дополнительная задача 1. Период затухающих колебаний системы составляет 0,2 с, а отношение амплитуд первого и шестого колебаний равно 13. Определите резонансную частоту данной колебательной системы.
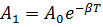
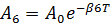
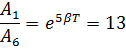
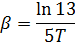
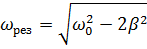
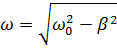
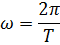
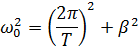
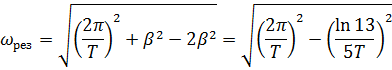
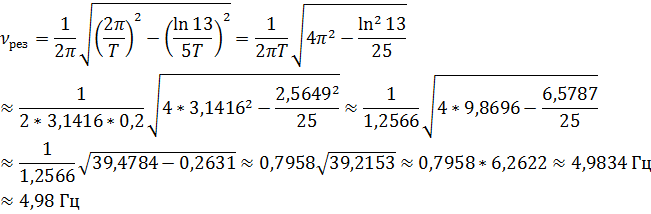
Ответ: 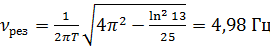 .
.
Дополнительная задача 2. За время, в течение которого система совершает 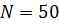 полных колебаний, амплитуда уменьшается в 2 раза. Определите добротность Q системы.
полных колебаний, амплитуда уменьшается в 2 раза. Определите добротность Q системы.
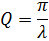
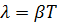
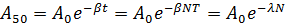
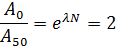
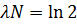
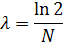
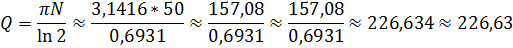
Ответ: 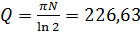 .
.
Дополнительная задача 3. Определите резонансную частоту колебательной системы, если собственная частота колебаний 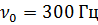 , а логарифмический декремент
, а логарифмический декремент 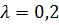 .
.
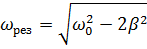
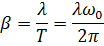
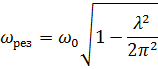
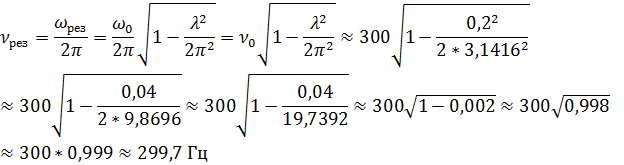
Ответ: 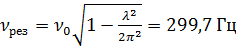 .
.
 2015-02-24
2015-02-24 9016
9016








