Одним из основных понятий математического анализа является функция.
Зачатки определения функции имелись у П. Ферма и Б. Паскаля. Впервые слово функция употребил Лейбниц в 1692 г.
Определение функции, наиболее близкое к современному, дал И. Бернулли в 1718 г.
До недавнего времени наиболее распространенным было следующее определение функции.
Переменная величина y называется функцией переменной величины x,если каждому значению х соответствует единственное определенное значение y. Записывается 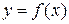 .
.
В настоящее время обычно употребляют определение функции, основанное на теории множеств.
Переменная величина y называется функцией переменной величины x с областью определения D и множеством значений E, если для любого значения х, принадлежащего множеству D (" x Î D)существует единственное значение y, принадлежащее множеству Е (y Î E) (рис. 3), т. е.
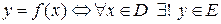 .
.

Рис. 3
Например, найти область определения и множество значений функции 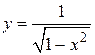 . Получаем
. Получаем 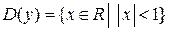 ,
, 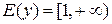 .
.
Если между множествами D и E можно установить взаимно однозначное соответствие, то существует обратная функция 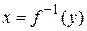 или
или 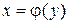 .
.
Если аргумент функции 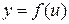 является в свою очередь функцией переменной величины х
является в свою очередь функцией переменной величины х 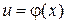 , то
, то 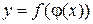 называется сложной функцией.
называется сложной функцией.
Здесь функции 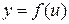 и
и 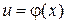 называются составляющими функциями.
называются составляющими функциями.
Например, 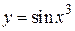 сложная функция, ее составляющие функции
сложная функция, ее составляющие функции 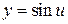 и
и 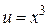 .
.
Основными элементарными функциями являются следующие:
1) 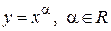 - степенная функция;
- степенная функция;
2) 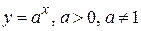 - показательная функция;
- показательная функция;
3) 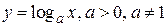 - логарифмическая функция;
- логарифмическая функция;
4) 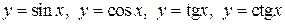 - тригонометрические функции;
- тригонометрические функции;
5) 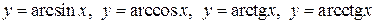 - обратные тригонометрические функции.
- обратные тригонометрические функции.
Функция называется элементарной, если она образована из основных элементарных с помощью конечного числа алгебраических действий: сложения, вычитания, умножения, деления, возведения в рациональную степень.
Например, 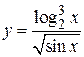 .
.
Функция называется алгебраической, если она образована из независимой переменной x с помощью конечного числа алгебраических действий: сложения, вычитания, умножения, деления, возведение в степень с рациональным показателем.
Функция называется трансцендентной, если она не является алгебраической.
Алгебраическая функция называется иррациональной, если она содержит операцию извлечение корня.
Функция называется рациональной, если она является алгебраической и не содержит корней независимой переменной.
Простейшей рациональной функцией является многочлен вида
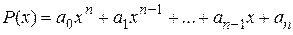 ,
,
где 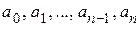 – числовые коэффициенты, х – независимая переменная, n – целое положительное число.
– числовые коэффициенты, х – независимая переменная, n – целое положительное число.
Любую рациональную функцию можно представить в виде отношения двух многочленов
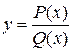 ,
,
где 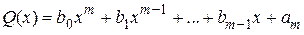 ,
, 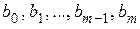 – числовые коэффициенты, m – целое положительное число.
– числовые коэффициенты, m – целое положительное число.
 2015-02-27
2015-02-27 1240
1240








