Окрестностью точки  называется любой интервал, содержащий эту точку.
называется любой интервал, содержащий эту точку.
d-окрестностью точки 
 называется интервал длиной 2d с центром в этой точке.
называется интервал длиной 2d с центром в этой точке.
В математическом анализе обычно рассматривается d-окрестность точки 
 , которая не содержит точку
, которая не содержит точку  (рис. 4).
(рис. 4).
Кратко записывается
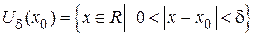
или 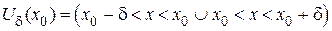 .
.

Рис. 4
Пусть в некоторой области D имеется предельная точка  .
.
Точка называется предельной, если любая, сколь угодно малая, ее окрестность содержит бесконечное множество точек этого множества. Из любого бесконечного множества точек можно выбрать бесконечное счетное множество, т.е. последовательность 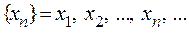 . Пусть эта последовательность такая, что с увеличением номера n члены последовательности
. Пусть эта последовательность такая, что с увеличением номера n члены последовательности 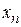 неограниченно приближаются к
неограниченно приближаются к  , но никогда не достигают его. Так что расстояние от точки х до точки
, но никогда не достигают его. Так что расстояние от точки х до точки  становится сколь угодно мало, но никогда не становится равным нулю. В этом случае говорят, что члены последовательности
становится сколь угодно мало, но никогда не становится равным нулю. В этом случае говорят, что члены последовательности 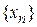 стремятся к
стремятся к  . Стремятся к
. Стремятся к  – значит неограниченно приближаются, но не достигают
– значит неограниченно приближаются, но не достигают  (рис. 5).
(рис. 5).
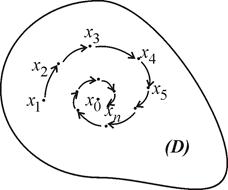
Рис. 5
Определение предела последовательности. Число b называется пределом последовательности 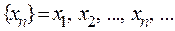 (
(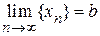 ), если для любого, сколь угодно малого, положительного d существует такое положительное число N, что если номер члена последовательности n > N, то
), если для любого, сколь угодно малого, положительного d существует такое положительное число N, что если номер члена последовательности n > N, то 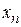 принадлежит d-окрестности числа b (
принадлежит d-окрестности числа b (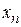 Î
Î 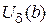 ).
).
Кратко с помощью кванторов можно записать
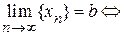
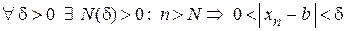 .
.
Например, доказать, что 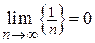 . Запишем последнее соотношение из определения предела и преобразуем его, учитывая, что
. Запишем последнее соотношение из определения предела и преобразуем его, учитывая, что 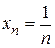 , а b = 0. Получим
, а b = 0. Получим 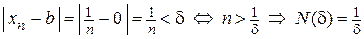 . Отсюда следует, что для того, чтобы член последовательности
. Отсюда следует, что для того, чтобы член последовательности 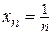 отличался от предела b = 0 меньше, чем на d = 0,001, его номер n должен быть больше
отличался от предела b = 0 меньше, чем на d = 0,001, его номер n должен быть больше 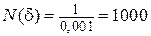 (n > 1000). При d = 0,0001 N (d) равняется
(n > 1000). При d = 0,0001 N (d) равняется 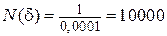 и т. д. Таким образом, для любого d можно выбрать N (d) такое, что
и т. д. Таким образом, для любого d можно выбрать N (d) такое, что 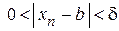 , если только n > N (d). Следовательно, предел этой последовательности равен нулю.
, если только n > N (d). Следовательно, предел этой последовательности равен нулю.
Теорема Больцано-Коши (без доказательства). Для того, чтобы последовательность 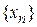 имела предел, необходимо и достаточно, чтобы для любого d > 0 существовало N (d)> 0 такое, что если n > N, m > N, то
имела предел, необходимо и достаточно, чтобы для любого d > 0 существовало N (d)> 0 такое, что если n > N, m > N, то 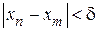 .
.
Теорема Вейерштрасса (без доказательства). Если последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет предел.
Последовательность 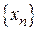 называется монотонно возрастающей (убывающей), если для любого n Î N
называется монотонно возрастающей (убывающей), если для любого n Î N 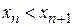 (
(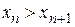 ).
).
 2015-02-27
2015-02-27 840
840








