2015-02-04
1738
Математические модели оптимизации
Сама по себе постановка задачи оптимизации проста и естественна: заданы множество Х и функция ¦(x),определённая на X, требуется найти точки минимума или максимума функции ¦ на X. Задачу на минимум запишем в виде:
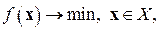(4.1)
При этом ¦ будем называть целевой функцией, X – допустимым множеством n - мерного пространства En, любой элемент х Î Х – допустимой точкой(допустимым решением, планом) задачи (4.1). Допустимая точка (допустимое решение), минимизирующая функцию цели, называется оптимальной точкой,точкой экстремума, оптимальным решением или просто решением. Если X совпадает со всем пространством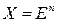 
, задача 4.1 называется задачей безусловной минимизации (без ограничений), в противном случае 
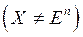– задачей условной минимизации (с ограничениями).
Ограничения подразделения:
а) на линейные (I, II) и нелинейные (III, IV) (рис. 4.1);
б) детерменированные (А, В) и стахостатические (группы кривых Сj) (рис. 4.2).
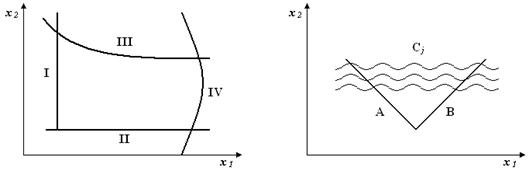
| Рис. 4.1. Линейные и нелинейные ог- раничения | Рис. 4.2. Детерменированные и стохас- тические ограничения |
Стохастические ограничения являются всевозможными, вероятными, случайными.
|
|
|
Необходимо подчеркнуть, что само понятие точки минимума, т.е. решения задачи (4.1), неоднозначно и требует уточнения.
Точка х *Î Х называется:
1) точкой глобального минимума функции ¦ на множестве Х или глобальным решением задачи (4.1), если
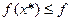(х), при " х Î Х; (4.2)
2) точкой локального минимума ¦ на Х или локальным решением задачи (4.1), если существует число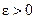 
такое, что
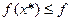(х), при всех 
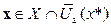; (4.3)
где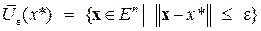 
– замкнутый шар радиуса 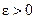с центром в х *.
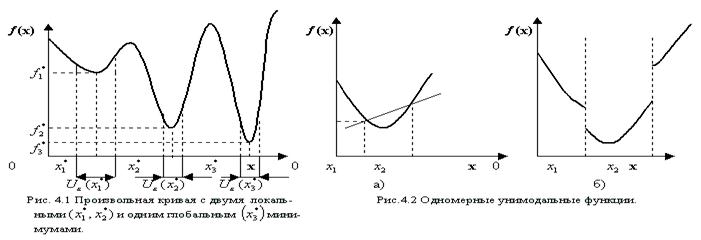
Рис. 4.3. Произволная кривая Рис. 4.4. Одномерные унимодаль-
с двумя локальными (х 1*, х 2*)и ные функции
одним глобальным (х 3*) минимумами
Таким образом, глобальный минимум – это наименьший из всех локальных минимумов. На рис. 4.3 показаны точки локальных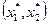 
и глобального 
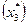минимумов для произвольной кривой ¦(x).
Задача оптимизации, в которой критерий оптимальности ¦(x) имеет в области Х единственный локальный минимум, называется одноэкстремальной (унимодальной) задачей оптимизации. Простейшими из унимодальных функций являются выпуклые функции (рис. 4.4, а). На рис. 4.4 приведены примеры унимодальных одномерных функций.
Задача оптимизации, в которой критерий оптимальности ¦(х) имеет несколько локальных минимумов, называется многоэкстремальной задачей оптимизации.
Обычные методы решений много экстремальных задач обеспечивают нахождение лишь отдельной особой точки, в которой частная производная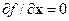 
. Такой точкой в зависимости от случайных обстоятельств (выбор начального приближения) может быть любой из локальных минимумов или точка перегиба. В связи с этим существенное значение имеет исследование условий, при которых решение обеспечивает нахождение глобального минимума.
|
|
|
Если неравенство в (4.2) или (4.3) выполняется как строгое при х ¹ х *, то говорят, что х * – точка строгого минимума (строгое решение) в глобальном или локальном смысле. Ясно, что глобальное решение является и локальным; обратное неверно.
Для отражения того факта, что точка х *Î Х является точкой глобального минимума функции ¦ на Х, будем использовать запись:
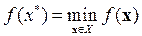
или эквивалентная ей запись
.
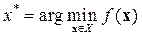При этом говорят, что точка х * реализует величину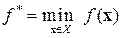 
,т.е. минимальное значение функции ¦ на Х. Множество всех точек глобального минимума ¦ на Х обозначим через
.
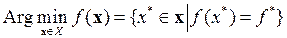Таким образом, arg min¦(x) – это просто произвольная точка из множества –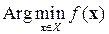 
.
При необходимости задачу минимизации можно заменить задачей максимизации или наоборот. Это объясняется тем, что минимум функции ¦ равен максимуму функции -¦, взятому с противоположным знаком, и достигаются оба эти экстремума при одних и тех же значениях переменных (рис. 4.5). В точке х * min¦(x *)= -max(-¦(x *)).
y=¦(x)
} min¦(x)
0 max¦(x){ x *. х
y= -¦(x)
Рис. 4.5. К постановке задачи оптимизации
Таким образом, если, например, задачу минимизации функции f (x 1, x 2,…, xn) при каких-либо ограничениях требуется заменить задачей максимизации, то достаточно вместо f (x 1, x 2,…, xn) взять в качестве целевой функцию - f (x 1, x 2,…, xn), найти максимум этой функции и заменить его знак на противоположный. Полученное значение будет оптимумом исходной задачи. По анологии с (4.1) будем записывать задачу максимизации функции ¦ на множестве Х в виде:
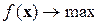, х Î Х (4.4)
Решения задач (4.1) и (4.4), т.е. точки минимума и максимума функции ¦ на Х называют также точками экстремума, а сами задачи (4.1) и (4.4) – экстремальными задачами.
