2015-02-27
1393
Интеграл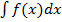 
можно упростить, введя вместо 
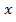новую переменную 
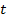, положив
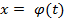(3)
Предложение 3. Для преобразования неопределенного интеграла к новой переменной 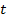по формуле (5.3) достаточно преобразовать его подынтегральное выражение:
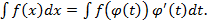(4)
Доказательство. Возьмем дифференциалы левой и правой части формулы (5.4), а также воспользуемся свойством 2 неопределенных интегралов и подстановкой (5.3), получим следующее:
.
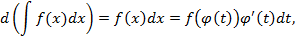
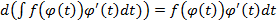Так как правые части равны, то и левые части тождественны. Отсюда следует справедливость формулы (5.4).
Пример 1.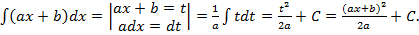 
Пример 2.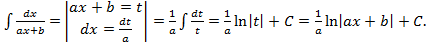 
Замечание. Новую переменную можно явно не записывать, а ввести постоянные и переменные под знаком дифференциала. Эту операцию называют преобразованием функции под знаком дифференциала.
Пример 3.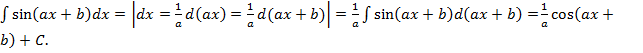 
Предложение 4. Пусть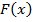 
некоторая первообразная для функции 
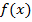. Тогда справедливо
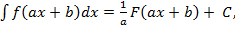(5)
где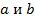 
- постоянные,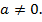 
Доказательство. Интеграл 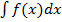можно записать в следующем в виде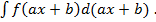 
Тогда по определению неопределенного интеграла имеем
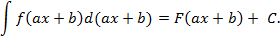
Но из определения дифференциала имеем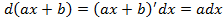 
. Тогда вынося постоянную 
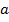за знак интеграла и деля правую и левую часть равенства на 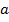, получим формулу (5).
