Перво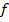образная функция и неопределенный интеграл

Пусть непрерывная на промежутке X функция.

Функция 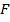называется первообразной функции 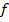на промежутке 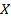, если 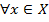существует конечная производная

.

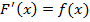Замечание 1. Первообразная 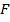как дифференцируемая на 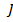функция непрерывна на .

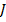Предложение 1. Если 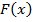первообразная 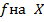, то и функция 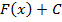есть первообразная 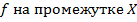, где 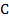произвольное постоянное число.

Доказательство. Пусть 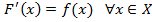. Отсюда следует

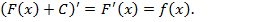
Предложение 2. Есл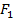и и 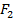– первообразные 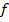на X, то существует постоянная С:

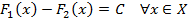(1)

Доказательство. Пусть

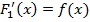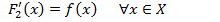, (2)

и пусть 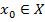-фиксированная точка. Положим 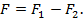По теореме Лагранжа и из равенства (2) 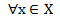имеем

,

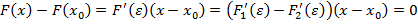где 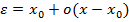. Отсюда следует

.

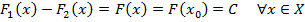Итак, первообразная 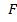на 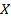, определена с точностью до постоянной .

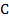Множество всех первообразных функций для функции 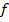на промежутке X называется неопределенным интегралом 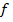на 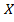. Обозначается 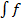или 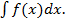В этом обозначении 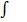называется знаком интеграла, 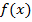– подынтегральной функцией, 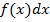– подынтегральным выражением.

Равенство 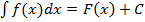будет обозначать, что 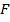- первообразная 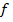на .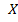

Пример. .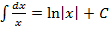

Действительно, .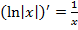

Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции. Интегрирование это обратное к дифференцированию операция.