1. Производная от неопределенного интеграла равна подынтегральной функции.
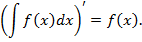
Доказательство. Непосредственно по определению неопределенного интеграла следует, что
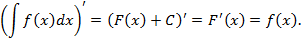
2. Дифференциал неопределенного интеграла равен подынтегральному выражению.
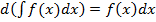 .
.
Доказательство. Из свойства 1 и по определению неопределенного интеграла и дифференциала, имеем
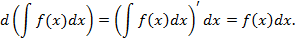
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного множителя.
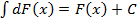 .
.
Доказательство. На основании свойства 2 и определения неопределенного интеграла, имеем
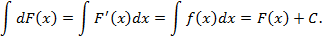
Следующие два свойства называются линейными свойствами неопределенного интеграла.
4. Постоянный множитель можно выносить за знак интеграла.
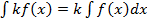 .
.
Доказательство. Введем новую функцию
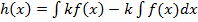 .
.
Возьмем производную этой функции и применяя свойство 1, получим
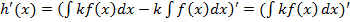 -
- 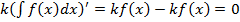 .
.
Из теоремы Лагранжа найдется такое число С,что 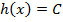 . Отсюда следует
. Отсюда следует
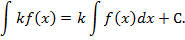
Здесь можно опустить постоянную С, так как неопределенный интеграл определяется с точностью до постоянного слагаемого.
5. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций
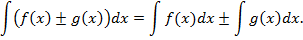
Доказательство аналогично свойству 4.
Таблица основных интегралов
Интегралы от элементарных функций называют табличными. Справедливость формул легко проверить дифференцированием.
1 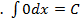 .
.
2. 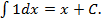
3. 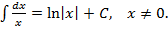
4. 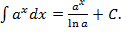
5. 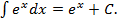
6. 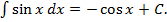
7. 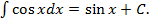
8. 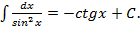
9. 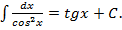
10. 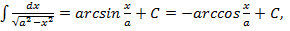
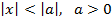
11. 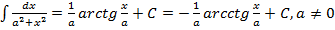
12. 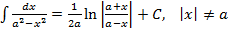
13. 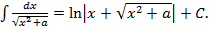
Пример. Докажем формулу 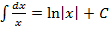 .
.
Пусть 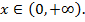 Производная правой части будет равна подынтегральной функции левой части.
Производная правой части будет равна подынтегральной функции левой части.
Действительно, 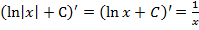 . Для
. Для 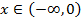 справедливо
справедливо
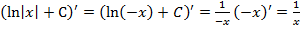 .
.
Аналогично доказываются остальные формулы таблицы.
4. Метод непосредственного интегрирования .
Вычисление интегралов с использованием основных правил интегрирования и таблицы неопределенных интегралов называется непосредственным интегрированием.
Пример 1. Найти 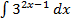 .
.
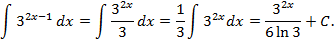
Пример 2. Найти 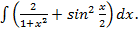
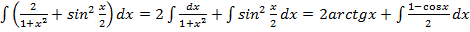 =
=
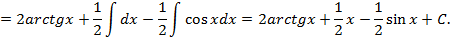
 2015-02-27
2015-02-27 15093
15093
