Рассмотрим интегралы вида 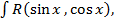 где
где 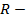 рациональная функция. Делаем замену переменного, полагая
рациональная функция. Делаем замену переменного, полагая 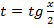 (
(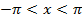 ), и следовательно,
), и следовательно,
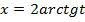 ,
, 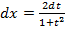 . Тогда
. Тогда 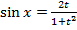 ,
, 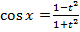 , откуда
, откуда
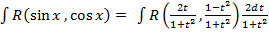 .
.
Пример. 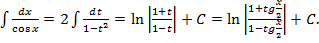
Можно применять и другие подстновки, а именно возможны следующие случаи:
если функция 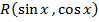 нечетно относительно
нечетно относительно 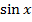 , т.е.
, т.е. 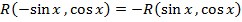 , то подстановка
, то подстановка 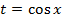 приводит к интегралу от рациональной функции;
приводит к интегралу от рациональной функции;
если функция 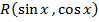 нечетно относительно
нечетно относительно 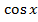 , т.е.
, т.е. 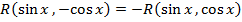 , то подстановка
, то подстановка 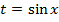 приводит к интегралу от рациональной функции;
приводит к интегралу от рациональной функции;
если функция 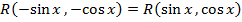 , то подстановка
, то подстановка 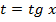 получают интеграл от рациональной функции
получают интеграл от рациональной функции
Пример 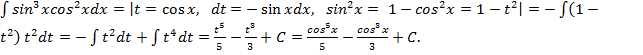
Рассмотрим интегралы вида 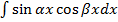 ,
, 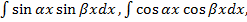 где
где 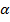 ,
, 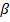 - некоторые действительные числа. С помощью известных формул для преобразования произведений тригонометрических функций в сумму, а именно
- некоторые действительные числа. С помощью известных формул для преобразования произведений тригонометрических функций в сумму, а именно
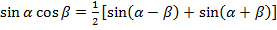 ,
,
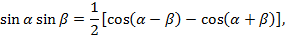
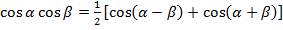 ,
,
такие интегралы сводятся к сумме простых табличных интегралов.
Пример 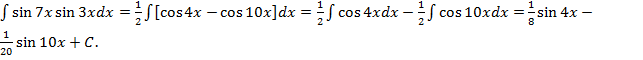
 2015-02-27
2015-02-27 1275
1275
