2015-02-27
602
Теорема 5. Пусть функци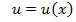и 
и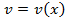 
имеют непрерывные производные на отрезке 
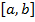. Тогда
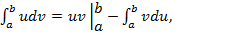(14)
где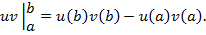 
Формула (14) называется формулой интегрирования по частям для определенного интеграла.
Доказательство. Так как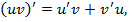 
то функция 
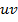является первообразной для функции 
.
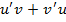По формуле Ньютона-Лейбница
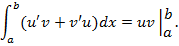
Преобразуем левую часть:
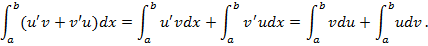
Отсюда вытекает формула (5.18).
6. Вычисление площадей плоских фигур.
Пусть функция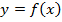 
неотрицательна и непрерывна на отрезке .
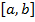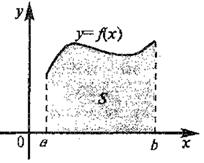
Рис.2
Рассмотрим на плоскости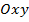 
фигуру, ограниченную графиком функции 
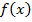на отрезке 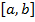, отрезком 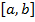и вертикальными прямым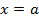и 
и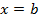 
. Эту фигуру называют криволинейной трапецией.
Тогда по геометрическому смыслу определенного интеграла площадь криволинейной трапеции равна определенному интегралу от функции 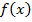на отрезке :
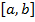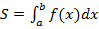. (15)
Пусть на отрезке 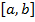заданы непрерывные функци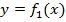и 
и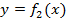 
такие, что 
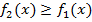. Тогда площадь 
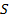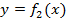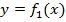фигуры, заключенные между кривыми и , на отрезке 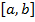вычисляется по формуле
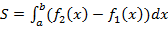. (16)
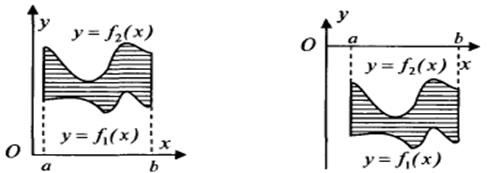
Рис.3
Пример 1. Найти площадь фигуры, ограниченной параболой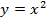 
, прямыми 
, 
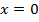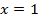и осью 
.
|
|
|
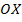По формуле (15) имеем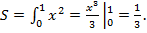 
Замечание 1. Если функция 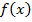неположительна и непрерывна на отрезке 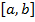. Тогда площадь под этой кривой на отрезке 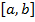задается формулой
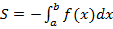. (17)
Замечание 2. Площадь фигуры, ограниченными линиями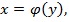 
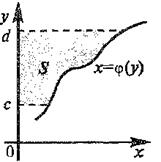
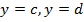, вычисляется по формуле
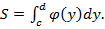(18)
Рис.4
