Непрерывна на отрезке 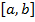 функция
функция 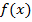 имеет на этом отрезке первообразную. Одной из первообразных является функция
имеет на этом отрезке первообразную. Одной из первообразных является функция
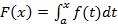 . (10)
. (10)
Так как всякая другая первообразная отличается от 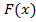 на постоянную величину, то связь между определенным и неопределенным интегралами имеет вид
на постоянную величину, то связь между определенным и неопределенным интегралами имеет вид
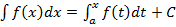 , (11)
, (11)
где 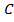 - некоторая постоянная.
- некоторая постоянная.
Подставляя в (11) 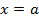 , с учетом свойства 1 определенного интеграла получаем
, с учетом свойства 1 определенного интеграла получаем
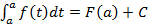 ,
, 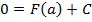 , откуда
, откуда 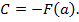
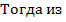 (11) имеем
(11) имеем
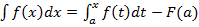 .
.
Полагая 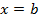 , получаем формулу
, получаем формулу
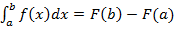 . (12)
. (12)
Равенство (12) называется основной формулой интегрального исчисления или формулой Ньютона-Лейбница.
Можно эту формулу записывать следующим образом.
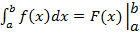 .
.
 2015-02-27
2015-02-27 938
938








