Рассмотрим тело, которое образуется при вращении вокруг оси 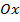 криволинейной трапеции, ограниченной сверху непрерывной и положительной на отрезке
криволинейной трапеции, ограниченной сверху непрерывной и положительной на отрезке 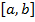 функцией
функцией 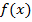 . Объем этого тела вращения определяется формулой
. Объем этого тела вращения определяется формулой
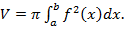 (19)
(19)
Если тело образованно вращением криволинейной трапеции вокруг оси 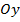 , то, выражая
, то, выражая 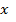 через y как обратную функцию, можем получить формулу для объема тела вращения:
через y как обратную функцию, можем получить формулу для объема тела вращения:
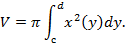
Пример 1. Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями 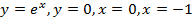 вокруг оси
вокруг оси 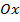 .
.
По формуле (5.23) имеем
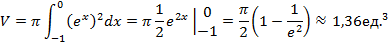
 2015-02-27
2015-02-27 574
574








