Основные свойства определенного интеграла

1. Интеграл, пределы интегрирования которого равны, равен нулю

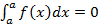(3)

Доказательство. Здесь рассматривается интеграл на отрезке нулевой длины.

2. От перестановки пределов интегрирования, знак интеграла поменяется.

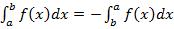(4)

при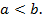

Доказательство следует из того, что при 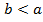длины частичных отрезков 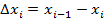будут иметь отрицательный знак в интегральной сумме.

3. Для любых чисел 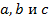имеет место равенство

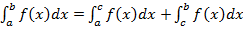. (5)

Возможны 2 случая.

a) Пусть 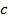лежит между 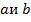. Тогда отрезок 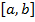можно разбить на два отрезка 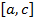и 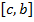и на этих отрезках можно составить интегральные суммы. Пределы этих интегральных сумм и будут определенными интегралами на каждом из этих отрезков, а их сумма есть определенный интеграл на отрезке 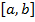, т.е. справедливо (5.9).

b) Пусть 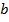лежит между 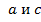. Из a) следует

,

.

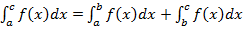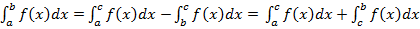4. Постоянный множитель можно выносить за знак определенного интеграла

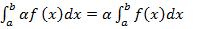(6)

:

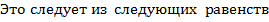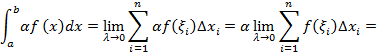
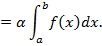
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:

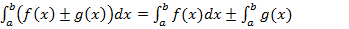(7)

Доказательство свойства 5 аналогично свойству 4.

6. Если 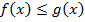всюду на отрезке 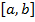, то

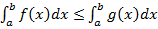(8)

Доказательство следует из справедливости неравенств:

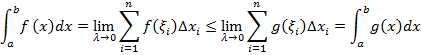
7. Если функция 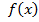нерерывна и ограничена на отрезке 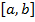, т.е.

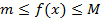, то

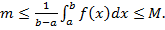(9)

По свойству 6 имеем

.

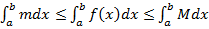Тогда из свойства 4 и геометрического свойства определенного интеграла

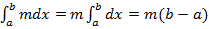и ,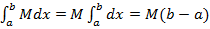

получаем требуемое неравенство (9).

Если 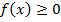всюду на отрезке 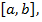то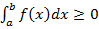

Доказательство аналогично свойству 6.