2015-02-27
2067
Комбинаторика - раздел математики, изучающий количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества.
Простейшая задача комбинаторики - подсчитать число подмножеств данного множества.
Комбинациями называют различные группы, составленные из каких-либо объектов, элементов.
Различают три вида комбинаций: перестановки, размещения и сочетания.
Перестановками из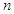 
элементов называют комбинации, содержащие все 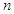элементов и отличающиеся между собой лишь порядком элементов.
Число перестановок из 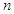элементов находится по формуле: 
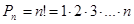(2)
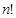– читается «эн факториал».
Принято считать, что 0! = 1.
Пример: Найти число перестановок из элементов
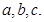Р3= 3! =1×2×3 = 6
, , , , ,
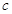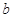
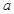
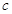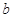
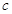
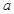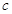
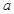
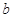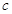
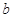
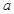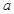
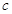
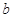
Размещениями из 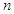элементов по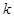 
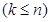называют такие комбинации, в каждую из которых входит 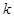элементов, взятых из данных 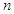элементов, и которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Число размещений из 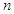элементов по 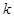находят по формуле:
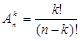(3)
Например: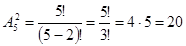 
Сочетаниями из 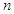элементов по 
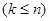называют комбинации, в каждую из которых входит 
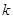элементов, взятых из данных 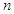элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из 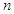элементов по 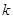находят по формуле:
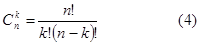
4. Статистическое определение вероятности.
На практике часто классическое определение вероятности не применимо, так как оно предполагает, что число элементарных исходов испытания конечно, а результат испытания можно представить в виде совокупности элементарных, равновозможных исходов. Поэтому используют статистическое определение вероятности. Относительная частота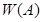 
события 
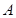есть отношение числа испытаний, в которых событие 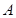появилось, к общему числу фактически произведенных испытаний 
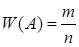, где
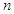- общее число произведенных испытаний,
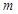- число появлений события А.
Задача. В партии из 1000 изделий товаровед обнаружил 15 бракованных. Чему равна относительная частота появления брака?
Решение: Обозначим через 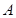- событие появление брака в данной партии. Всего произведенных изделий в партии 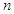= 1000, а бракованных 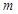- 15.
Согласно определению имеем: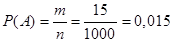 
Сравнивая определения вероятности и относительной частоты, заметим, что в определении вероятности не требуется, чтобы испытания проводились в действительности,. А в определении относительной частоты предполагается, что испытания были проведены, т.е. вероятность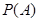 
вычисляют до опыта, а относительную частоту 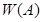– после опыта.
Длительные наблюдения показали, что относительные частоты появления события при многократно повторяющихся опытах мало отличаются друг от друга, а последовательность частот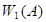 
, 
,..., 
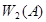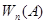,... имеет предел. Этот предел называется статистической вероятностью события.
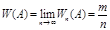
Для подтверждения факта приближения относительной частоты к вероятности проводились массовые опыты бросания монеты. При 4040 бросках относительная частота появления герба равнялась 0,5069, а при 23000 бросках - 0,5005, т.е практически не отличалась от вероятности. этого события, равной 0,5.
5. Теорема сложения вероятностей несовместных и совместных событий.
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий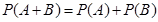 
. (1)
Следствие. Сумма вероятностей несовместных событий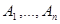 
, образующих полную группу, равна единице: 
.
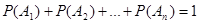Определение. Событие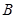 
называют зависимым от события 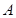, если появление события 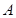изменяет вероятность появления события .
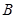Вероятность события 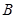, найденная при условии, что событие 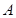произошло, называется условной вероятностью события 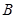и обозначается 
.
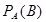Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
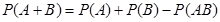(4)
Для трех совместных событий имеем:
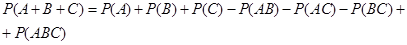
События 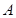, 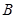и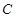 
могут быть как зависимыми, так и независимыми, тогда 
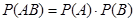(для независимых событий) и 
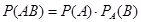(для зависимых событий).
6. Теорема умножения вероятностей для зависимых
