Определение. Два события называются независимыми, если вероятность появления одного из них не зависит от того, появилось или не появилось другое событие.
Теорема. Вероятность совместного появления двух зависимых событий 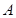 и
и 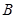 равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событиеуже наступило, т.е.
равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событиеуже наступило, т.е.
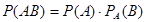 или
или 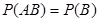
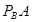 (3)
(3)
Теорема умножения вероятностей может быть распространена на любое число m зависимых событий 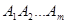 .
.
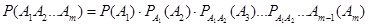 ,
,
причем вероятность последующего события вычисляется в предположении, что все предыдущие произошли.
Задача 1. В коробке 2 белых и 3 синих ручки. Из коробки вынимают подряд две ручки. Найти вероятность того, что обе ручки белые.
Решение. событие 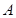 - обе ручки белые.
- обе ручки белые.
событие 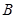 - появление первой белой ручки,
- появление первой белой ручки,
событие 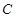 - появление второй белой ручки.
- появление второй белой ручки.
Тогда 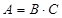 .
.
Так как первая ручка не возвращается в коробку, т.е. состав коробки изменился, то события 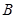 и
и 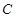 зависимые.
зависимые.
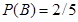 ;
;
Вероятность события 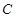 находим в предположении, что
находим в предположении, что 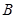 уже произошло, т.е.
уже произошло, т.е. 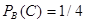 .
.
Искомая вероятность
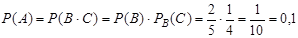
Несколько событий называются взаимно независимыми (или независимыми в совокупности), если каждое из них и любая комбинация, составленная из остальных (части или всех) событий, являются независимыми событиями.
Если события 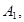
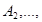
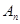 взаимно независимы, то и противоположные их события
взаимно независимы, то и противоположные их события 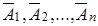 также взаимно независимы.
также взаимно независимы.
Теорема. Вероятность произведения нескольких взаимно независимых событий равна произведению вероятностей этих событий.
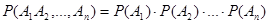
Для двух событий 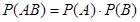 (2)
(2)
7. Вероятность гипотез. Формулы Бейеса
 2015-02-27
2015-02-27 844
844








