2015-02-27
677
Свойство 1. Значения интегральной функции распределения принадлежат отрезку. Значения интегральной функции распределения принадлежат отрезку [0,1]: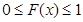 
.
Свойство 2. Функция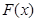 
есть неубывающая функция,
т.е.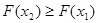 
, если 
.
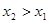Свойство 3. Вероятность того, что случайная величина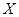 
примет значение, заключенное в интервале 
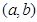, равна приращению интегральной функции на этом интервале: 
.
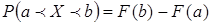Следствие 1. Вероятность того, что случайная величина 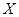примет одно определенное значение, например 
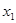, равна нулю: 
.
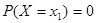Следствие 2. Если все возможные значения случайной величины 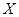принадлежат интервалу 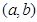, то
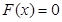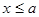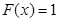при 
,
при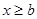 
Дифференциальной функцией распределения вероятностей называют первую производную от интегральной функции: 
(2)
Часто вместо термина «дифференциальная функция» используют термин «плотность вероятности».
