Главный вектор пространственной системы сил определяется так же, как в плоской статике: это вектор 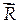 , равный векторной сумме всех сил системы:
, равный векторной сумме всех сил системы:
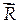 = =  1+ 1+  2+...+ 2+...+  n= n= 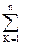  k. k. | (1.39) |
Модуль R главного вектора пространственной системы сил вычисляется по следующим формулам:
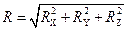 , , | (1.40) |
где
R X = 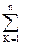 F KX, R Y = F KX, R Y = 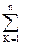 F KY, R Z = F KY, R Z = 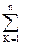 F KZ. F KZ. | (1.41) |
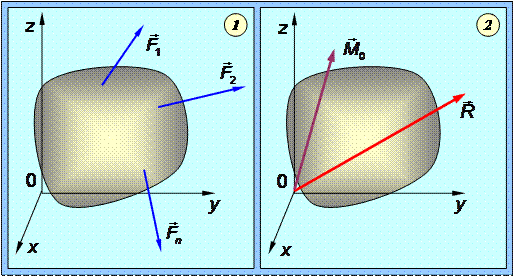
Рис.1.40
Главный момент системы сил называется вектор 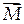 0, равный сумме векторных моментов всех сил относительно некого центра (точки О) (рис.1.40):
0, равный сумме векторных моментов всех сил относительно некого центра (точки О) (рис.1.40):
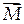 0 = 0 =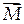 0 ( 0 ( 1 )+ 1 )+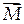 0 ( 0 ( 2 )+...+ 2 )+...+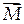 0 ( 0 ( n )= n )= 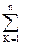 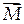 0 ( 0 ( k). k). | (1.42) |
Вектор 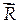 не зависит от выбора центра О, а вектор
не зависит от выбора центра О, а вектор 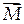 0 при изменении положения центра О может в общем случае изменяться.
0 при изменении положения центра О может в общем случае изменяться.
В соответствии с принципом суперпозиции (наложением) величина главного момента M 0 системы сил относительно центра O (начала координат) и его проекции (главные осевые моменты) вычисляются по формулам:
M X = 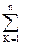 (y К F КZ - z К F КY ); M Y = (y К F КZ - z К F КY ); M Y = 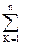 (z К F КX - x К F КZ ); M Z = (z К F КX - x К F КZ ); M Z = 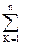 (x К F КY - y К F КX ); (x К F КY - y К F КX ); 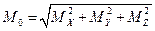 . . | (1.43) |
Здесь x К, y К, z К, - координаты точки приложения силы  K.
K.
Для простых случаев главные осевые моменты могут определяться геометрически
|
|
|
Пример.
К вершинам куба (рис.1.41) с длиной ребра a приложена система четырех сил, действующих вдоль ребер куба и имеющих одинаковые модули: F 1= F 2= F 3= F 4= F.
Определить главный вектор этой системы сил и её главный момент относительно вершины О.
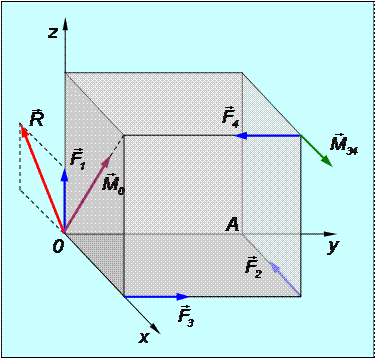
Рис.1.41
Решение. Введем координатную систему Oxyz, оси которой ориентированы вдоль ребер куба.
Силы  3,
3,  4 образуют пару сил с векторным моментом
4 образуют пару сил с векторным моментом  34, направленным в положительном направлении оси Ox (точка приложения вектора
34, направленным в положительном направлении оси Ox (точка приложения вектора  34 может быть выбрана произвольно) и равным по модулю M 34 = F · a. Следовательно, силы
34 может быть выбрана произвольно) и равным по модулю M 34 = F · a. Следовательно, силы  3 и
3 и  4 можно не учитывать при вычислении проекций главного вектора
4 можно не учитывать при вычислении проекций главного вектора 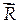 .
.
Определяем проекции главного вектора 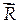 :
:
R X = F 1x + F 2x = 0 - F 2 = - F;
R Y = F 1y + F 2y = 0;
R Z = F 1z + F 2z = F + 0 = F.
Модуль главного вектора:
R = (R X + R Y + R Z) 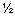 =
= 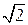 F.
F.
Вычисляем проекции главного момента 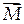 0 относительно точки О, определяя осевые моменты сил
0 относительно точки О, определяя осевые моменты сил  1 и
1 и  2 геометрически (напомним, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости) и проецируя векторный момент
2 геометрически (напомним, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости) и проецируя векторный момент 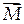 34 на оси координат:
34 на оси координат:
MX = MX(  1) + MX(
1) + MX(  2) + (
2) + ( 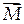 34)X= 0 + 0 + M34 = F a;
34)X= 0 + 0 + M34 = F a;
MY = MY(  1) + MY(
1) + MY(  2) + (
2) + ( 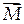 34)Y = 0 + 0 + 0 = 0;
34)Y = 0 + 0 + 0 = 0;
MZ = MZ(  1) + MZ(
1) + MZ(  2) + (
2) + ( 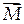 34)z = 0 + F·OA + 0 = F a;
34)z = 0 + F·OA + 0 = F a;
Модуль главного момента:
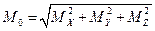 =
= 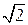 F·a.
F·a.
Таким образом, для заданной системы сил её главный вектор 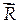 и главный момент
и главный момент 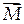 0 относительно точки О равны по модулю R =
0 относительно точки О равны по модулю R = 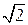 F; M 0=
F; M 0= 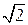 F · a, лежат в плоскости Oxz и образуют с осью Oz углы в 45° (см. рис.1.41).
F · a, лежат в плоскости Oxz и образуют с осью Oz углы в 45° (см. рис.1.41).
 2015-10-14
2015-10-14 29417
29417
