Четырехпроводные трехфазные цепи (рисунок 4.4) используются при напряжениях до 1000 В во внутренних и наружных проводках стационарных объектов. При соединении обмоток генератора звездой концы фаз Х, Y, Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью). Концы фаз нагрузки x, y, z так же соединяются в нейтральной точке n. Начала фаз нагрузки (а, b, c) подключаются к началам фаз генератора (А, В, С).
Провода, соединяющие начала фаз генератора с нагрузкой называются линейными, а токи протекающие в этих проводах – линейными токами (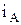 ,
, 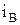 ,
, 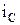 ). Напряжение между двумя линейными проводами называют линейным напряжением (
). Напряжение между двумя линейными проводами называют линейным напряжением (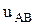 ,
, 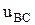 ,
, 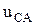 ). Провод, соединяющий нейтраль генератора и нейтраль приемника, называют нейтральным проводом, а ток протекающий в этом проводе – током нейтрального провода (
). Провод, соединяющий нейтраль генератора и нейтраль приемника, называют нейтральным проводом, а ток протекающий в этом проводе – током нейтрального провода (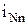 ). Ток, протекающий от начала к концу фазы нагрузки, называется фазным током нагрузки (
). Ток, протекающий от начала к концу фазы нагрузки, называется фазным током нагрузки (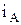 ,
, 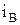 ,
, 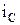 ), при соединении нагрузки звездой фазные токи равны линейным.
), при соединении нагрузки звездой фазные токи равны линейным.
Напряжение между началом и концом фазы называют фазным напряжением (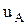 ,
, 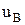 ,
, 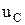 ). Фазным током генератора является ток, протекающий через фазную обмотку статора. Расположение фаз по часовой стрелке называется прямым чередованием фаз (А, В, С), а против часовой – обратным чередованием (А, С, В).
). Фазным током генератора является ток, протекающий через фазную обмотку статора. Расположение фаз по часовой стрелке называется прямым чередованием фаз (А, В, С), а против часовой – обратным чередованием (А, С, В).
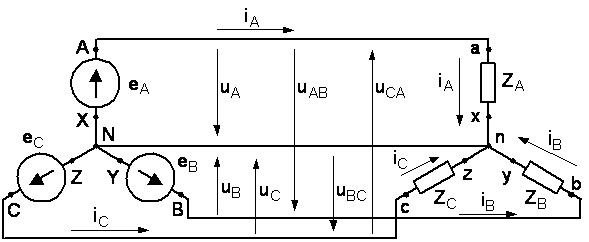
Рисунок 4.4 - Четырехпроводная трехфазная цепь (звезда с нейтральным проводом)
Если комплексные сопротивления фаз нагрузки равны между собой (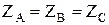 ), то такую нагрузку называют симметричной. Если это условие не выполняется то нагрузку называют несимметричной.
), то такую нагрузку называют симметричной. Если это условие не выполняется то нагрузку называют несимметричной.
Если пренебречь сопротивлениями линейных и нейтрального проводов, то фазные напряжения на нагрузке будут равны фазным ЭДС источника (генератора):
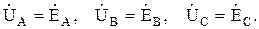
Линейные напряжения можно определить по второму закону Кирхгофа:
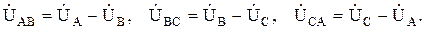
Токи в каждой фазе приемника определяться по формулам:
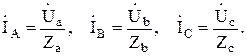
В соответствии с приведенными уравнениями построена топографическая векторная диаграмма (рисунок 4.5) для симметричной четырехпроводной трехфазной цепи. Так как комплексные сопротивления фаз нагрузки равны, то фазные токи имеют одинаковую величину и сдвинуты относительно векторов фазных напряжений на один и тот же угол. Из рассмотрения треугольника напряжений образованного векторами 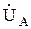 ,
, 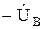 и
и 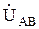 следует, что значение линейного напряжения определяется, как:
следует, что значение линейного напряжения определяется, как: 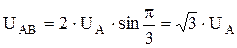 , то есть при соединении звездой линейное напряжение в
, то есть при соединении звездой линейное напряжение в 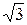 раз больше фазного. Кроме того, из векторной диаграммы следует, что при симметричной нагрузке ток нейтрального провода равный сумме векторов фазных токов равен нулю:
раз больше фазного. Кроме того, из векторной диаграммы следует, что при симметричной нагрузке ток нейтрального провода равный сумме векторов фазных токов равен нулю: 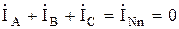 . То есть при симметричной нагрузке ток в нейтральном проводе не протекает, следовательно, необходимость в этом проводе отпадает. Поэтому при подключении к трехфазной системе симметричной нагрузки фазы которой соединены звездой (трехфазные электродвигатели, электрические печи и т. п.) применяется трехпроводная трехфазная цепь, показанная на рисунке 4.6. Векторная диаграмма этой цепи ничем не отличается от векторной диаграммы четырехпроводной трехфазной цепи.
. То есть при симметричной нагрузке ток в нейтральном проводе не протекает, следовательно, необходимость в этом проводе отпадает. Поэтому при подключении к трехфазной системе симметричной нагрузки фазы которой соединены звездой (трехфазные электродвигатели, электрические печи и т. п.) применяется трехпроводная трехфазная цепь, показанная на рисунке 4.6. Векторная диаграмма этой цепи ничем не отличается от векторной диаграммы четырехпроводной трехфазной цепи.
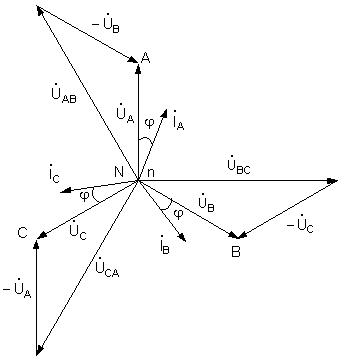
Рисунок 4.5 - Топографическая векторная диаграмма для симметричной четырехпроводной трехфазной цепи
В несимметричном режиме, когда 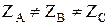 , режимы работы четырехпроводной и трехпроводной трехфазных цепей значительно отличаются. В четырехпроводной цепи (рисунок 4.4), благодаря нейтральному проводу напряжения на каждой из фаз нагрузки будут неизменными и равными соответствующим фазным напряжениям источника, как по величине, так и по фазе. Так как комплексные сопротивления фаз не равны то токи в фазах будут различными, и ток нейтрального провода будет отличаться от нуля:
, режимы работы четырехпроводной и трехпроводной трехфазных цепей значительно отличаются. В четырехпроводной цепи (рисунок 4.4), благодаря нейтральному проводу напряжения на каждой из фаз нагрузки будут неизменными и равными соответствующим фазным напряжениям источника, как по величине, так и по фазе. Так как комплексные сопротивления фаз не равны то токи в фазах будут различными, и ток нейтрального провода будет отличаться от нуля: 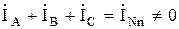 . Векторная диаграмма для несимметричной четырехпроводной трехфазной цепи приведена на рисунке 4.7.
. Векторная диаграмма для несимметричной четырехпроводной трехфазной цепи приведена на рисунке 4.7.
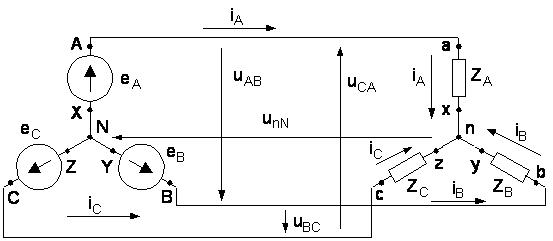
Рисунок 4.6 - Трехпроводная трехфазная цепь при соединении нагрузки звездой
В трехпроводной трехфазной цепи фазные напряжения приемника не будут равны соответствующим фазным напряжениям источника. В этом случае между нейтральными точками источника и приемника возникает напряжение 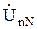 - напряжение смещения нейтрали. Для определения напряжения смещения нейтрали можно воспользоваться методом двух узлов:
- напряжение смещения нейтрали. Для определения напряжения смещения нейтрали можно воспользоваться методом двух узлов:
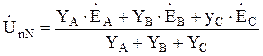 ,
,
где 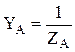 ,
, 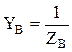 ,
, 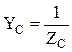 - комплексные проводимости фаз нагрузки. Зная напряжение смещения нейтрали и фазные напряжения источника можно определить фазные напряжения на нагрузке:
- комплексные проводимости фаз нагрузки. Зная напряжение смещения нейтрали и фазные напряжения источника можно определить фазные напряжения на нагрузке:
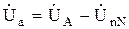 ,
, 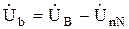 ,
, 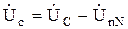 .
.
Векторная диаграмма соответствующая несимметричному режиму работы трехпроводной цепи показана на рисунке 4.8. Из векторной диаграммы видно, что несимметрия нагрузки в трехпроводной цепи приводит к значительному искажению системы фазных напряжений на нагрузке, причем фазные напряжения могут значительно превышать свои номинальные значения. Поэтому в трехпроводных цепях, при соединении нагрузки звездой допустим только симметричный режим, то есть комплексные сопротивления фаз нагрузки должны быть равны.
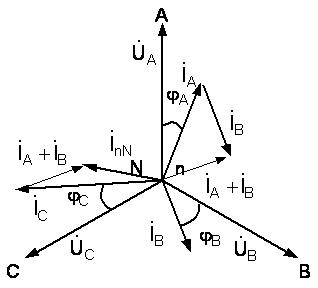
Рисунок 4.7 - Векторная диаграмма для несимметричной четырехпроводной трехфазной цепи
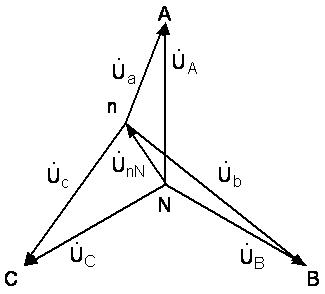
Рисунок 4.8 - Векторная диаграмма для несимметричной трехпроводной трехфазной цепи
 2015-02-27
2015-02-27 27396
27396








