Основной магнитный поток трансформатора - 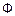 , замыкается через ферромагнитный сердечник и сцеплен с витками первичной и вторичной обмоток. Помимо основного потока, токи обмоток создают магнитные потоки рассеяния (рисунке 5.1), которые сцеплены с витками только одной обмотки – первичной или вторичной. Эти потоки рассеяния наводят в обмотках трансформатора дополнительные ЭДС, которые называются ЭДС рассеяния -
, замыкается через ферромагнитный сердечник и сцеплен с витками первичной и вторичной обмоток. Помимо основного потока, токи обмоток создают магнитные потоки рассеяния (рисунке 5.1), которые сцеплены с витками только одной обмотки – первичной или вторичной. Эти потоки рассеяния наводят в обмотках трансформатора дополнительные ЭДС, которые называются ЭДС рассеяния - 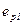 и
и 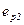 . Таким образом для первичной обмотки трансформатора напряжение питающей сети уравновешивается ЭДС
. Таким образом для первичной обмотки трансформатора напряжение питающей сети уравновешивается ЭДС 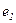 от основного магнитного потока, ЭДС
от основного магнитного потока, ЭДС 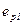 от потока рассеяния и падением напряжения на активном сопротивлении обмотки -
от потока рассеяния и падением напряжения на активном сопротивлении обмотки - 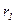 . Так как напряжения, ЭДС и токи в первичной обмотке трансформатора являются синусоидальными, то можно записать уравнение электрического состояния для первичной обмотки в комплексной форме:
. Так как напряжения, ЭДС и токи в первичной обмотке трансформатора являются синусоидальными, то можно записать уравнение электрического состояния для первичной обмотки в комплексной форме:
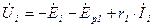 . (5.10)
. (5.10)
ЭДС рассеяния обычно учитывают с помощью дополнительной индуктивности рассеяния 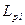 :
:
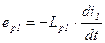 ,
, 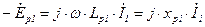 . (5.11)
. (5.11)
Тогда уравнение электрического состояния первичной обмотки запишется в виде:
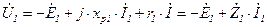 , (5.12)
, (5.12)
где 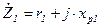 - комплексное сопротивление первичной обмотки. Аналогично может быть получено уравнение электрического равновесия для вторичной обмотки, с учетом того, что напряжение на вторичной обмотке равно ЭДС
- комплексное сопротивление первичной обмотки. Аналогично может быть получено уравнение электрического равновесия для вторичной обмотки, с учетом того, что напряжение на вторичной обмотке равно ЭДС 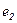 наводимой основным потоком за вычетом ЭДС рассеяния вторичной обмотки
наводимой основным потоком за вычетом ЭДС рассеяния вторичной обмотки 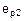 и падения напряжения на активном сопротивлении вторичной обмотки
и падения напряжения на активном сопротивлении вторичной обмотки 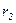 :
:
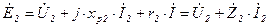 , (5.13)
, (5.13)
где 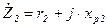 - комплексное сопротивление вторичной обмотки.
- комплексное сопротивление вторичной обмотки.
Падения напряжения в обмотках 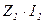 и
и 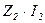 составляют обычно не более нескольких процентов от напряжений
составляют обычно не более нескольких процентов от напряжений 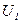 и
и 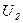 . Поэтому с некоторым приближением можно считать, что в нагруженном трансформаторе сохраняется равенство
. Поэтому с некоторым приближением можно считать, что в нагруженном трансформаторе сохраняется равенство 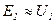 и
и 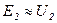 . При этом допущении амплитуда основного магнитного потока:
. При этом допущении амплитуда основного магнитного потока:
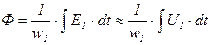 , (5.14)
, (5.14)
считается постоянной во всех режимах работы, так как напряжение питающей сети 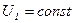 . Магнитный поток трансформатора определяется совместным действием намагничивающих сил первичной и вторичной обмоток. Причем намагничивающая сила вторичной обмотки направлена противоположно намагничивающей силе первичной, то есть стремится размагнитить сердечник. Так как магнитный поток в сердечнике постоянен, то и алгебраическая сумма намагничивающих сил обмоток должна оставаться постоянной, это равенство выражается уравнением намагничивающих сил трансформатора:
. Магнитный поток трансформатора определяется совместным действием намагничивающих сил первичной и вторичной обмоток. Причем намагничивающая сила вторичной обмотки направлена противоположно намагничивающей силе первичной, то есть стремится размагнитить сердечник. Так как магнитный поток в сердечнике постоянен, то и алгебраическая сумма намагничивающих сил обмоток должна оставаться постоянной, это равенство выражается уравнением намагничивающих сил трансформатора:
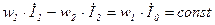 , (5.15)
, (5.15)
где 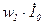 - намагничивающая сила в режиме холостого хода, когда тока во вторичной обмотке нет, а ток холостого хода первичной обмотки равен току намагничивания
- намагничивающая сила в режиме холостого хода, когда тока во вторичной обмотке нет, а ток холостого хода первичной обмотки равен току намагничивания 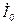 . Если разделить левую и правую части уравнения (5.15) на
. Если разделить левую и правую части уравнения (5.15) на 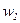 получим:
получим:
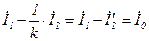 , (5.16)
, (5.16)
где 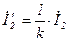 - приведенный ток вторичной обмотки трансформатора.
- приведенный ток вторичной обмотки трансформатора.
В соответствии с уравнениями (5.12, 5.13, 5.16) построена векторная диаграмма трансформатора, работающего под нагрузкой (рисунке 5.2).
Построение векторной диаграммы удобно начинать с вектора основного потока 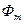 . На векторной диаграмме используется приведенная ЭДС вторичной обмотки
. На векторной диаграмме используется приведенная ЭДС вторичной обмотки 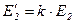 в этом случае векторы
в этом случае векторы 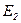 и
и 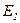 совпадают по величине и направлению (отстают от вектора магнитного потока на p/2). При введении понятия о приведенных ЭДС, напряжениях и токах необходимо найти приведенные сопротивления вторичной обмотки, равные отношению приведенных напряжений к приведенным токам:
совпадают по величине и направлению (отстают от вектора магнитного потока на p/2). При введении понятия о приведенных ЭДС, напряжениях и токах необходимо найти приведенные сопротивления вторичной обмотки, равные отношению приведенных напряжений к приведенным токам:
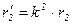 ,
, 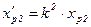 . (5.17)
. (5.17)
Таким образом, уравнение (4.13) для вторичной обмотки трансформатора на векторной диаграмме заменяется соответствующим уравнением для приведенных величин:
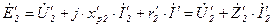 , (5.18)
, (5.18)
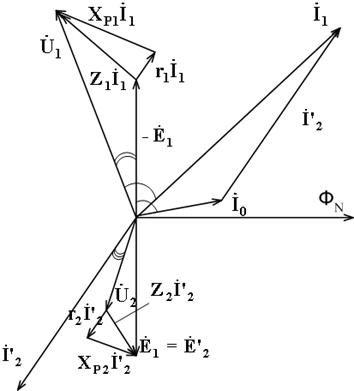
Рисунок 5.2 - Векторная диаграмма трансформатора,
работающего под нагрузкой
На векторной диаграмме для наглядности составляющие падения напряжения на активных и индуктивных сопротивлениях первичной и вторичной обмоток показаны преувеличенно большими, на самом деле их величины не превышают нескольких процентов от напряжений  и
и 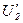 .
.
 2015-02-27
2015-02-27 2935
2935