Дифференциальное уравнение первого порядка. Задача Коши
Дифференциальное уравнение первого порядка имеет вид:
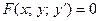 (8.2)
(8.2)
Если это уравнение разрешено относительно 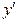 , то это уравнение имеет вид:
, то это уравнение имеет вид: 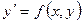 или
или 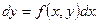
Для дифференциального уравнения существует несколько видов решений: общее решение, частное решение и особое решение.
Общим решением дифференциального уравнения первого порядка называется функция 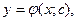 зависящая от
зависящая от 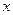 и от одной произвольной постоянной, и обращающая это уравнение в тождество.
и от одной произвольной постоянной, и обращающая это уравнение в тождество.
Частным решением дифференциального уравнения первого порядка называется всякое решение 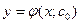 , полученное из общего решения при фиксированном значении
, полученное из общего решения при фиксированном значении 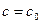 .
.
Задача Коши - задача нахождения частного решения дифференциального уравнения при заданном начальном условии: 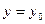 при
при 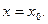
Tеорема 8.1. Если в уравнении 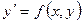 функция
функция 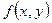 и ее частная производная
и ее частная производная 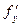 непрерывны в некоторой области D на плоскости
непрерывны в некоторой области D на плоскости 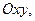 содержащей некоторую точку
содержащей некоторую точку 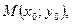 то существует единственное решение этого уравнения
то существует единственное решение этого уравнения 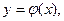 удовлетворяющее условию
удовлетворяющее условию 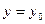 при
при 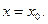
Геометрический смысл теоремы заключается в следующем: существует и при том единственная функция 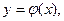 график которой проходит через точку
график которой проходит через точку 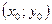 .
.
Уравнения с разделяющимися переменными
Дифференциальное уравнение вида
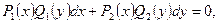
где 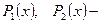 функции только от
функции только от 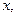 а
а 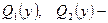 функции только от
функции только от 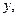 называется уравнением с разделяющимися переменными (ДУсРП).
называется уравнением с разделяющимися переменными (ДУсРП).
Для отыскания решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функции переменной 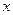 окажутся в одной части равенства, а переменной у – в другой. Затем проинтегрировать обе части полученного равенства и получить общее решение исходного уравнения:
окажутся в одной части равенства, а переменной у – в другой. Затем проинтегрировать обе части полученного равенства и получить общее решение исходного уравнения:
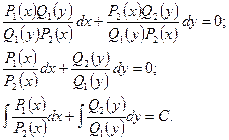
Пример. Решить уравнение: 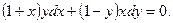
Решение. Это ДУсРП, т.к. при 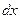 и при
и при 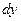 стоят произведение функций, каждая из которых зависит либо только от
стоят произведение функций, каждая из которых зависит либо только от 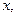 либо только от
либо только от 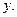
Разделим обе части уравнения на произведение 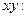
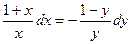 или
или 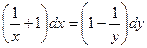
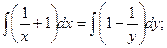
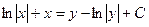 или
или 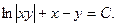
Однородные дифференциальные уравнения
Понятие однородного уравнения связано с однородными функциями.
Функция 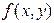 называется однородной функцией n -го порядка относительно переменных x и y, если при любом числа
называется однородной функцией n -го порядка относительно переменных x и y, если при любом числа 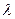 имеет место равенство:
имеет место равенство: 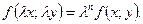
Пример: Выяснить, являются ли однородными функции:
а)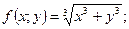 б)
б)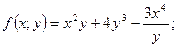 в)
в) 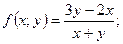 г)
г) 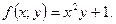
Решение. а) Так как 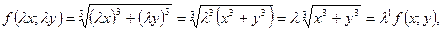 то данная функция однородная 1-го порядка.
то данная функция однородная 1-го порядка.
б) Так как 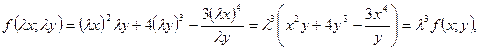 то данная функция однородная 3-го порядка.
то данная функция однородная 3-го порядка.
в) Так как 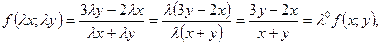 то данная функция однородная 0-го порядка.
то данная функция однородная 0-го порядка.
г) Так как 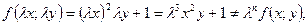 то данная функция неоднородная.
то данная функция неоднородная.
Однородным дифференциальным уравнением первого порядка (ОДУ) называется уравнение вида: 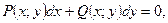 где
где 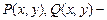 однородные функции одинакового порядка
однородные функции одинакового порядка
или
Дифференциальное уравнение вида 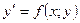 называется однородным, если функция
называется однородным, если функция 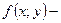 однородная нулевого порядка.
однородная нулевого порядка.
Решение ОДУ проводится путем введения новой переменной 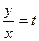 или
или 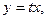 что позволяет свести это уравнение к ДУсРП.
что позволяет свести это уравнение к ДУсРП.
Пример. Решить уравнение 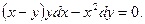
Решение. Убедимся, что это ОДУ. Действительно,
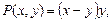 а
а 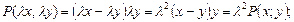
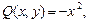 а
а 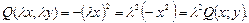
Преобразуем исходное уравнение к виду: 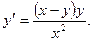
Введем новую переменную 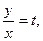 тогда
тогда 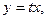
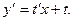
Получим: 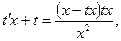
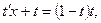
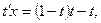
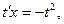
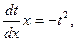 разделим переменные
разделим переменные
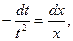 проинтегрируем
проинтегрируем
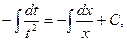
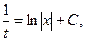 пусть
пусть 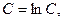
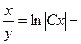 общее решение ОДУ.
общее решение ОДУ.
Линейные дифференциальные уравнения. Уравнение Бернулли
Линейным дифференциальным уравнением первого порядка (ЛДУ) называется уравнение, линейное (то есть первой степени) относительно y и 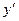 вида:
вида:
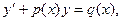 (8. 5)
(8. 5)
где 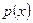 и
и 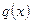 заданные функции от
заданные функции от 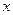 (или постоянные).
(или постоянные).
Особенность ЛДУ первого порядка – искомая функция у и ее производная 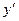 входят в уравнение в первой степени, не перемножаясь между собой.
входят в уравнение в первой степени, не перемножаясь между собой.
Решение ЛДУ сводится к решению двух ДУсРП подстановкой 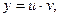 где
где 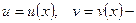 функции от
функции от 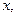 одна из которых может быть выбрана произвольно, а другая определяется уравнением (…).
одна из которых может быть выбрана произвольно, а другая определяется уравнением (…).
Пусть 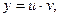 тогда
тогда 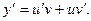 Подставим в уравнение (…). Получим
Подставим в уравнение (…). Получим
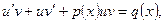
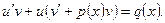
Выберем функцию 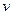 таковой, что выражение в скобках обратилось в нуль:
таковой, что выражение в скобках обратилось в нуль: 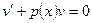 . Это будет первое вспомогательное уравнение – ДУсРП относительно функции
. Это будет первое вспомогательное уравнение – ДУсРП относительно функции 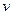 . Решая его, получим частное решение –
. Решая его, получим частное решение – 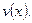 (можем взять любое частное решение, например, при
(можем взять любое частное решение, например, при 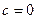 ). Подставим
). Подставим 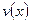 в уравнение… получим второе вспомогательное уравнение –ДУсРП относительно функции
в уравнение… получим второе вспомогательное уравнение –ДУсРП относительно функции 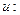
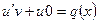 или
или 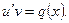 . Решая второе уравнение, находим общее решение в виде
. Решая второе уравнение, находим общее решение в виде 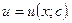 . Подставляя, таким образом найденные, функции
. Подставляя, таким образом найденные, функции 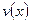 и
и 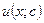 в формулу
в формулу 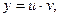 окончательно получаем решение ЛДУ:
окончательно получаем решение ЛДУ: 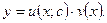
Пример. Найти общее решение уравнения 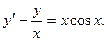
Решение. Это ЛДУ, в котором 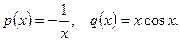 . Будем искать решение в виде
. Будем искать решение в виде 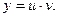 Подставляя
Подставляя 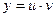 и
и 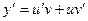 в исходное уравнение, получим:
в исходное уравнение, получим:
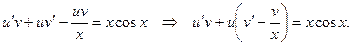
Решаем первое вспомогательное уравнение 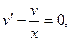 получим
получим
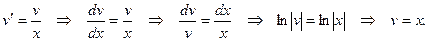
Подставляя найденную функцию 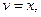 получим второе вспомогательное уравнение
получим второе вспомогательное уравнение 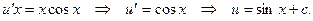 . Таким образом, общее решение исходного ЛДУ имеет вид
. Таким образом, общее решение исходного ЛДУ имеет вид 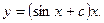
Уравнение Бернулли имеет вид: 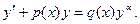 Оно отличается от ЛДУ тем, что в правую часть входит множитель функция
Оно отличается от ЛДУ тем, что в правую часть входит множитель функция 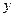 в некоторой степени, и решается так же, как и ЛДУ подстановкой
в некоторой степени, и решается так же, как и ЛДУ подстановкой 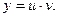
 2014-01-25
2014-01-25 2323
2323
