Для описания движения твердых тел необходимо вычислять тензор инерции относительно разных точек. Так, например, тело может вращаться вокруг различных неподвижных точек и, соответственно, осей. Чтобы избавиться от необходимости каждый раз вычислять интегралы (5.22), (5.23), найдем связь между центральным тензором инерции 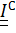 , который является неотъемлемым, вычисленным или измеренным атрибутом тела, и тензором инерции в некоторой точке
, который является неотъемлемым, вычисленным или измеренным атрибутом тела, и тензором инерции в некоторой точке 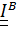 (рис. 5.7).
(рис. 5.7).
Подставляя в определение тензора 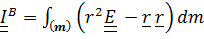 выражения
выражения 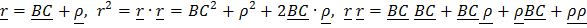 ,
,
получим: 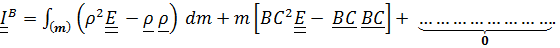 .
.
Все невыписанные слагаемые равны нулю, поскольку они содержат равный нулю множитель 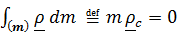 (постоянные вектор
(постоянные вектор 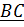 и тензор
и тензор 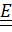 выносятся из интегралов). Таким образом, получили обобщенную теорему Гюйгенса – Штейнера:
выносятся из интегралов). Таким образом, получили обобщенную теорему Гюйгенса – Штейнера:
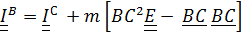 . (5.24)
. (5.24)
| Рис. 5.7. Теорема Гюйгенса– Штейнера |
Пусть
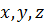
– оси с началом в точке
В и базисными векторами
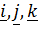
, а
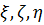 –
– параллельные им оси с началом в центре масс (
центральные оси) c координатами
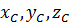
.
Умножая (5.24) слева и справа скалярно на 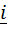 , получим формулу связи для осевых моментов инерции:
, получим формулу связи для осевых моментов инерции:
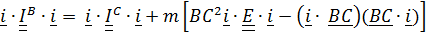 , или
, или
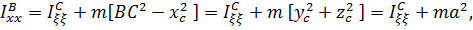 (5.25)
(5.25)
где 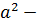 квадрат расстояния между осями
квадрат расстояния между осями 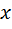 и
и 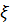 .
.
Умножая (5.24) слева на 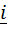 и справа на
и справа на 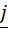 , получим формулу связи для центробежных моментов инерции:
, получим формулу связи для центробежных моментов инерции:
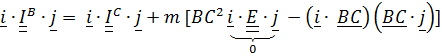 , или
, или
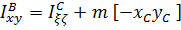 . (5.26)
. (5.26)
Разумеется, формулы (5.25) и (5.26) легко записываются и для других осей. Заметим также, что поскольку осевые моменты инерции не зависят от положения точек на осях, часто в формулах (5.25) «имена» точек В и С опускаются.
Из (5.25) следует, что осевые моменты инерции минимальны, если оси центральные (вспомним о центре масс, как о точке, «ближайшей» ко всем точкам тела).
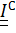 , который является неотъемлемым, вычисленным или измеренным атрибутом тела, и тензором инерции в некоторой точке
, который является неотъемлемым, вычисленным или измеренным атрибутом тела, и тензором инерции в некоторой точке 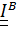 (рис. 5.7).
(рис. 5.7).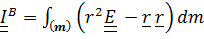 выражения
выражения 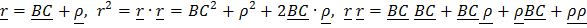 ,
,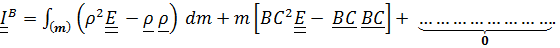 .
.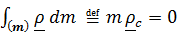 (постоянные вектор
(постоянные вектор 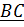 и тензор
и тензор 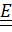 выносятся из интегралов). Таким образом, получили обобщенную теорему Гюйгенса – Штейнера:
выносятся из интегралов). Таким образом, получили обобщенную теорему Гюйгенса – Штейнера: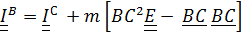 . (5.24)
. (5.24)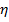
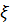
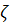
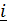
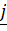
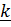
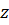
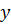
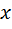
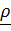
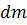
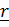
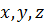 – оси с началом в точке В и базисными векторами
– оси с началом в точке В и базисными векторами 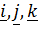 , а
, а 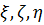 – параллельные им оси с началом в центре масс (центральные оси) c координатами
– параллельные им оси с началом в центре масс (центральные оси) c координатами 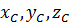 .
. 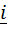 , получим формулу связи для осевых моментов инерции:
, получим формулу связи для осевых моментов инерции: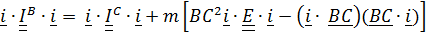 , или
, или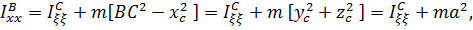 (5.25)
(5.25)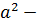 квадрат расстояния между осями
квадрат расстояния между осями 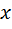 и
и 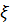 .
.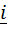 и справа на
и справа на 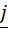 , получим формулу связи для центробежных моментов инерции:
, получим формулу связи для центробежных моментов инерции: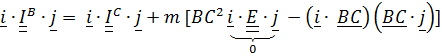 , или
, или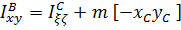 . (5.26)
. (5.26) 2015-02-04
2015-02-04 1594
1594








