Эллипсоид инерции

Тензору инерции, как и всякому симметричному тензору, можно поставить в соответствие наглядный геометрический объект – так называемую тензорную поверхность (рис. 5.9). Пусть 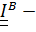тензор инерции в точке В. Построим квадратичную форму и приравняем ее единице:

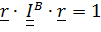. (5.27)

Это уравнение поверхности, описываемой вектором 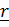с началом в точке В, которая для положительного тензора является эллипсоидом. Действительно, записав 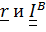в главных осях 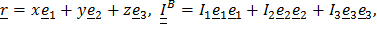получим в каноническом виде 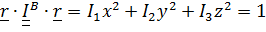или

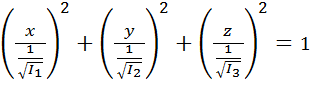. (5.27а)

Уравнение (5.27) – уравнение эллипсоида с полуосями, равными .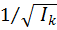

Момент инерции 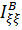относительно оси 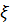с ортом , проходящей через точку 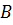и пересекающей эллипсоид в точке 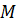, обратно пропорционален квадрату расстояния :

.

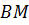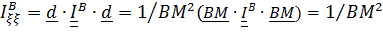Так как протяженное в каком–либо направлении тело имеет относительно оси, совпадающей с этим направлением, наименьший момент инерции, то эллипсоид инерции приблизительно повторяет форму тела.

Вычислим дифференциал от уравнения (5.27): 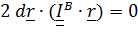, отсюда следует, что вектор 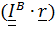перпендикулярен к эллипсоиду, поскольку вектор 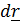лежит в касательной плоскости к поверхности.

Например, кинетический момент тела, вращающегося вокруг точки В, равен 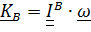, поэтому 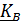направлен по нормали к поверхности эллипсоида в точке его пересечения с мгновенной осью вращения, проведенной через точку В.

Если тело обладает осью симметрии «N» – го порядка, т. е. переходит «само в себя» при повороте на угол 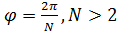(см. рис. 5.8,в), то «вмороженный» в него эллипсоид инерции обладает тем же свойством и, следовательно, является эллипсоидом вращения с двумя, по меньшей мере, равными полуосями; т. е. тензор инерции 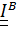трансверсально–изотропный.