Начнем с определения: Если для тензора второго ранга 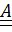 существует вектор
существует вектор 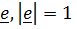 такой, что
такой, что 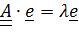 , то число
, то число 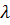 называется главным (собственным) значением тензора,
называется главным (собственным) значением тензора, 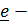 собственным вектором, а ось, задаваемая
собственным вектором, а ось, задаваемая 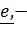 главной осью тензора.
главной осью тензора.
Теорема о приведении тензора инерции к главным осям. Тензор инерции, как и любой симметричный тензор, имеет тройку ортогональных собственных векторов 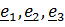 и тройку вещественных собственных значений (главных моментов)
и тройку вещественных собственных значений (главных моментов) 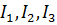 , причем:
, причем:
1) если собственные значения различны, то собственные векторы определяются единственным образом и тензор инерции имеет вид:
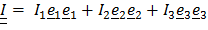 ;
;
2) если два собственных значения равны, например, 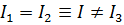 , то однозначно определяется собственный вектор
, то однозначно определяется собственный вектор 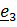 , а
, а 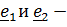 любые перпендикулярные к
любые перпендикулярные к 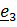 (и друг к другу); в этом случае
(и друг к другу); в этом случае
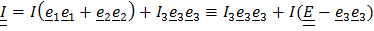 ;
;
такой тензор называется трансверсально–изотропным: он не изменяется при вращении тела вокруг оси изотропии, задаваемой 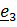 ;
;
3) Если равны все собственные значения 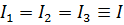 , то
, то 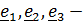 любая ортонормированная тройка и тензор инерции называется шаровым:
любая ортонормированная тройка и тензор инерции называется шаровым:
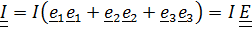 .
.
Эта теорема доказывается в курсе линейной алгебры как теорема о собственных числах (значениях) и собственных векторах симметричной матрицы.
Применительно к тензору инерции ее содержание сводится к тому, что существует, по меньшей мере, одна тройка главных осей, т. е. осей, относительно которых центробежные моменты инерции равны нулю, и тензор инерции в этих осях имеет вид: 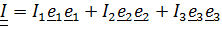 .
.
Поскольку ориентация тройки осей задается тремя параметрами (например, углами Эйлера), то возможность сделать равными нулю три центробежных момента существует.
В некоторых случаях, когда тело обладает каким-либо видом симметрии, то согласно физическому принципу Кюри–Неймана этой же симметрией должен обладать и тензор инерции; тогда главные оси могут быть найдены из соображений симметрии. Так, например, если тело обладает плоскостью симметрии Bxz, то перпендикулярная ей ось y является главной (рис. 5.8,а). Действительно, центробежные моменты 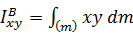 и
и 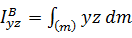 равны нулю, поскольку каждому элементу
равны нулю, поскольку каждому элементу 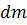 с координатами
с координатами 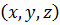 соответствует симметричный с координатами
соответствует симметричный с координатами 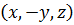 . Если имеется еще одна плоскость симметрии
. Если имеется еще одна плоскость симметрии 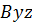 , перпендикулярная первой, то ось
, перпендикулярная первой, то ось 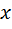 (а, следовательно, и
(а, следовательно, и 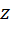 ) тоже главная:
) тоже главная: 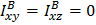 ,так что тензор инерции для любой точки В, находящейся на линии пересечения этих плоскостей, имеет вид:
,так что тензор инерции для любой точки В, находящейся на линии пересечения этих плоскостей, имеет вид:
 .
.
Если тело осесимметричное (рис. 5.8,б), то любая плоскость, содержащая ось 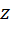 , является плоскостью симметрии и, в дополнение ко всему изложенному ясно, что
, является плоскостью симметрии и, в дополнение ко всему изложенному ясно, что 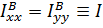 ; так что тензор инерции трансверсально–изотропный:
; так что тензор инерции трансверсально–изотропный:
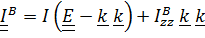 .
.
Если тело обладает осью симметрии «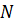 » – го порядка, т. е. тело переходит «само в в себя» при повороте на угол
» – го порядка, т. е. тело переходит «само в в себя» при повороте на угол 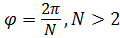 (на рис. 5.8,в
(на рис. 5.8,в 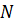 =5), то и в этом случае тензор инерции
=5), то и в этом случае тензор инерции 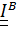 трансверсально–изотропный.
трансверсально–изотропный.
| Рис. 5.8. Симметричные тела |
| Рис. 5.9.Эллипсоид инерции |
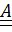 существует вектор
существует вектор 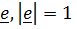 такой, что
такой, что 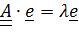 , то число
, то число 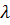 называется главным (собственным) значением тензора,
называется главным (собственным) значением тензора, 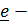 собственным вектором, а ось, задаваемая
собственным вектором, а ось, задаваемая 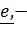 главной осью тензора.
главной осью тензора.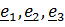 и тройку вещественных собственных значений (главных моментов)
и тройку вещественных собственных значений (главных моментов) 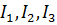 , причем:
, причем: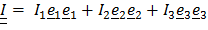 ;
;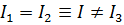 , то однозначно определяется собственный вектор
, то однозначно определяется собственный вектор 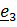 , а
, а 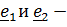 любые перпендикулярные к
любые перпендикулярные к 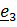 (и друг к другу); в этом случае
(и друг к другу); в этом случае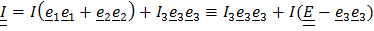 ;
;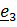 ;
;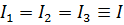 , то
, то 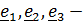 любая ортонормированная тройка и тензор инерции называется шаровым:
любая ортонормированная тройка и тензор инерции называется шаровым: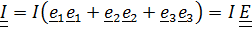 .
.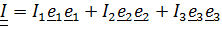 .
.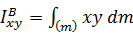 и
и 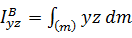 равны нулю, поскольку каждому элементу
равны нулю, поскольку каждому элементу 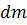 с координатами
с координатами 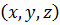 соответствует симметричный с координатами
соответствует симметричный с координатами 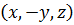 . Если имеется еще одна плоскость симметрии
. Если имеется еще одна плоскость симметрии 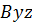 , перпендикулярная первой, то ось
, перпендикулярная первой, то ось 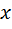 (а, следовательно, и
(а, следовательно, и 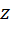 ) тоже главная:
) тоже главная: 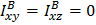 ,так что тензор инерции для любой точки В, находящейся на линии пересечения этих плоскостей, имеет вид:
,так что тензор инерции для любой точки В, находящейся на линии пересечения этих плоскостей, имеет вид: .
.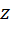 , является плоскостью симметрии и, в дополнение ко всему изложенному ясно, что
, является плоскостью симметрии и, в дополнение ко всему изложенному ясно, что 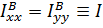 ; так что тензор инерции трансверсально–изотропный:
; так что тензор инерции трансверсально–изотропный: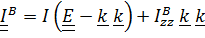 .
.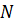 » – го порядка, т. е. тело переходит «само в в себя» при повороте на угол
» – го порядка, т. е. тело переходит «само в в себя» при повороте на угол 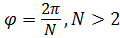 (на рис. 5.8,в
(на рис. 5.8,в 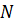 =5), то и в этом случае тензор инерции
=5), то и в этом случае тензор инерции 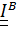 трансверсально–изотропный.
трансверсально–изотропный.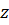
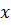
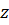
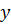
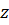

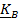
 2015-02-04
2015-02-04 852
852








