2015-02-04
619
Из определения тензора инерции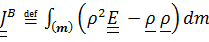 
, вычисляемого в актуальном положении твердого тела, ясно, что тензор инерции зависит от времени. Разложим вектор 
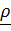и единичный тензор по базису 
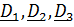, жестко связанному с телом (рис. 5.6):
.
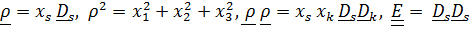Тензор инерции примет вид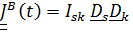 
, где координаты 
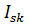постоянные
величины, а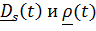 
– это повернутые вместе с телом постоянные векторы
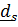и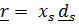 
в отсчетном, например, при 
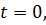положении. Таким образом, 
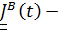это повернутый вместе с телом («вмороженный» в тело) постоянный тензор, т. е. 
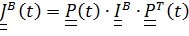, где
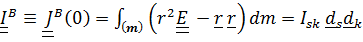. (5.20)
| Рис. 5.6. Тензор инерции |
| B |
|
|
|
|
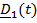
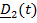
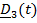
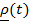
| B |
|
|
|
|
|
|
|
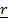
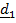
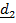
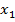
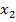
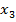
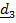
| dm |
Далее мы будем говорить о постоянном тензоре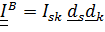 
, координаты которого называются моментами инерции. Из (5.20) ясно, что тензор инерции симметричный 
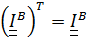, т. е. 
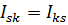. Формально координаты 
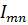тензора в ортонормированном базисе вычисляются с помощью скалярного умножения тензора слева на 
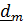, а справа на 
:
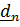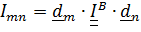. (5.21)
Из (5.20) получим:
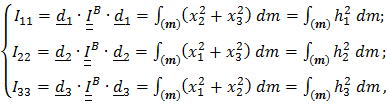(5.22)
где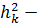 
квадрат расстояния от элемента 
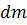до «k»– й оси,
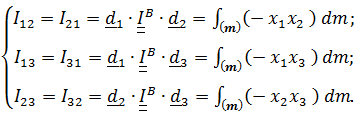. (5.23)
Моменты инерции (5.22) называются осевыми, а(5.23) – центробежными.
Из (5.22) следуют своеобразные «правила треугольника»:
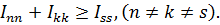
Например,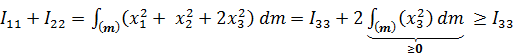 
,
причем ясно, что равенство возможно только в тех случаях, когда у всех точек тела координата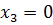 
; например, если тело – бесконечно тонкий стержень или бесконечно тонкая пластина.
