| Рис. 5.11. Вращение вокруг неподвижной оси |
| a) |
| B |
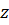 |
| A |
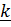 |
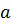 |
| A |
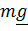 |
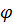 |
| б) |
Пусть твердое тело вращается вокруг неподвижной оси
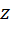 (рис. 5.11,a).
(рис. 5.11,a). Уравнение второго фундаментального закона имеет вид:
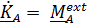 , или
, или 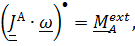
где точка А – любая точка на оси вращения, 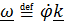 – вектор угловой скорости.
– вектор угловой скорости.
Если нас интересует только угол поворота 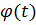 , достаточно найти одну лишь проекцию на ось
, достаточно найти одну лишь проекцию на ось 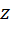 , для чего умножим скалярно обе части уравнения на орт
, для чего умножим скалярно обе части уравнения на орт 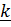 и внесем его в производную:
и внесем его в производную:
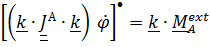 .
.
По определению, 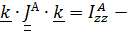 осевой момент инерции, причем это постоянная величина, а
осевой момент инерции, причем это постоянная величина, а  момент относительно оси
момент относительно оси 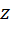 . Таким образом, получили дифференциальное уравнение вращения вокруг неподвижной оси:
. Таким образом, получили дифференциальное уравнение вращения вокруг неподвижной оси:
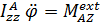 (5.29)
(5.29)
Если ось подвеса горизонтальна и внешними воздействиями являются сила
тяжести и, разумеется, опорные воздействия, с которыми ось подвеса действует на тело, то тело называют физическим маятником (рис. 5.11,б). В этом случае уравнение (5.29) принимает вид нелинейного уравнения
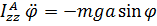 , которое может быть проинтегрировано либо численно, либо в так называемых эллиптических функциях. Уравнение малых колебаний, под которыми будут пониматься движения, описываемые линейными дифференциальными уравнениями, получим, положив
, которое может быть проинтегрировано либо численно, либо в так называемых эллиптических функциях. Уравнение малых колебаний, под которыми будут пониматься движения, описываемые линейными дифференциальными уравнениями, получим, положив 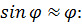
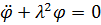 , (5.30)
, (5.30)
где обозначено 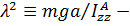 квадрат собственной частоты.
квадрат собственной частоты.
Решение уравнения (5.30) имеет вид: 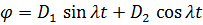 , где константы
, где константы 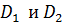 определяются из начальных условий
определяются из начальных условий 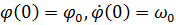 .
.
Ясно, что измеряя собственную частоту 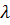 (или период
(или период 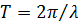 ), можно экспериментально найти момент инерции
), можно экспериментально найти момент инерции 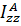 .
.
 2015-02-04
2015-02-04 707
707








