Дифференциальное уравнение (7.1)имеет вид:
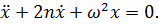 (7.7)
(7.7)
По методу Эйлера решение будем искать в виде 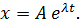 Подставляя его в (7.7), получим характеристическое уравнение:
Подставляя его в (7.7), получим характеристическое уравнение:
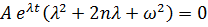 ,
,
откуда определяются собственные числа 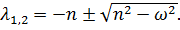
Общее решение имеет вид:
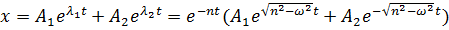 , (7.7а)
, (7.7а)
| а) |
| Рис. 7.4. Затухающие колебания |
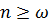
|
| x |
| t |
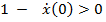
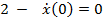
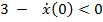
|
| б) |
| T |
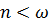
|
где
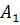 и
и 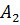 определяются из начальных условий. Рассмотрим три возможных случая.
определяются из начальных условий. Рассмотрим три возможных случая.
а) Большое сопротивление: 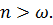 В этом случае собственные числа
В этом случае собственные числа 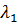 и
и 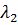 вещественные, и решение (7.7а) тоже вещественное; его для удобства часто записывают в виде:
вещественные, и решение (7.7а) тоже вещественное; его для удобства часто записывают в виде:
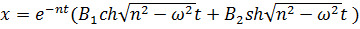 , (7.7б)
, (7.7б)
где 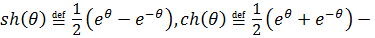 гиперболические функции, удобные для определения постоянных из начальных условий, поскольку
гиперболические функции, удобные для определения постоянных из начальных условий, поскольку
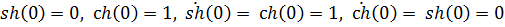 .
.
Подставим начальные условия:
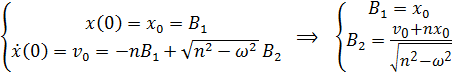 ,и
,и
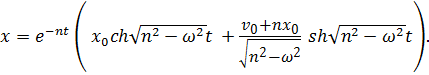 (7.7в)
(7.7в)
Эскизы графиков движения в зависимости от начальных условий могут иметь вид, представленный на (рис. 7.4,а). Эти движения принято называть апериодическими (непериодическими) колебаниями, хотя они и не имеют колебательного характера.
б) Предельно–апериодическое движение: 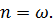 В этом случае собственные числа
В этом случае собственные числа 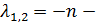 кратные и, как известно из математики, частные решения имеют вид
кратные и, как известно из математики, частные решения имеют вид 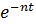 и
и 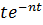 , так что общее решение
, так что общее решение 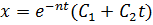 . Впрочем, это решение, как и в случае резонанса (см. раздел 7.1.2), получается предельным переходом при
. Впрочем, это решение, как и в случае резонанса (см. раздел 7.1.2), получается предельным переходом при 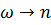 из общего решения (7.7в). Замечая, что для малых
из общего решения (7.7в). Замечая, что для малых 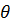
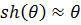 , получим:
, получим:
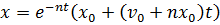
Характер движения вполне описывается эскизами (см.рис. 7.4,а).
в) Малое сопротивление: 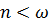 (затухающие периодические колебания). Собственные числа
(затухающие периодические колебания). Собственные числа 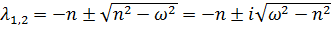 комплексные и формально записанное решение
комплексные и формально записанное решение 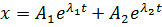 тоже комплексное. С помощью формулы Эйлера
тоже комплексное. С помощью формулы Эйлера 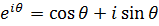 оно принимает вид:
оно принимает вид:
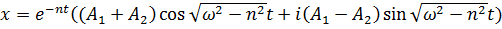 .
.
Разумеется, если найти постоянные из вещественных начальных условий, мнимая часть решения «исчезнет» (станет равной нулю):
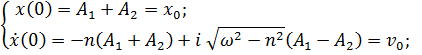
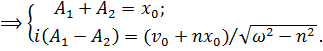 .
.
Таким образом,
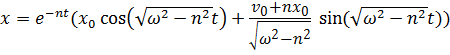 . (7.7г)
. (7.7г)
Обычно это вещественное решение сразу записывают в виде суммы вещественной и мнимой частей, умноженных на константы, определяемые из начальных условий: 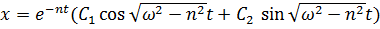 .
.
Действительно, если комплексная функция является решением линейного уравнения с вещественными коэффициентами, то решениями являются ее вещественная и мнимая части.
Решение может быть записано в виде одной гармоники (рис. 7.4,б):
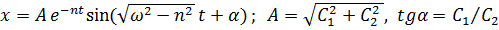 .
.
Частота колебаний 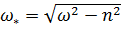 , «период»
, «период» 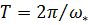 .
.
 2015-02-04
2015-02-04 463
463








