2015-02-27
463
Пусть функция f(x) задана таблично:
Таблица 3
| X | X0 | X1 | X2 | … | Xn |
| F(x) | Y0 | Y1 | Y2 | … | Yn |
В процессе решения задачи необходимо для некоторой промежуточной точки х получить значение f(x). Так как вид функции f(x) неизвестен, требуется найти многочлен Qm(x), который в заданных точках х0, х1,…, xn совпадал со значениями функции f(x), т. е.
Qm(x0)=f(x0),
Qm(x1)=f(x1), (3.3)
Qm(xn)=f(xn),
где Qm(x)=c0φ0(x)+c1φ1(x)+…+cmφm(x) называется интерполяционным многочленом.
Условие (3.3) называется условием интерполяции. Точки х0, х1,…, хn называются узлами интерполяции. В остальных точках отрезка [x0, xn] области определения функции f(x) многочлен Qm(x) приближенно представляет значения f(x) с той или иной степенью точности. Задача построения Qm(x) при условии (3.3) называется задачей интерполирования.
Условие (3.3) необходимо, но не достаточно для нахождения единственного многочлена Qm(x), так как при данном условии через точки f(xi) (i=0,…,n) можно провести более одного Qm(x):
y 
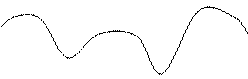Q"m(x) Q'm(x)
 | |||||||
 | |||||||
 | |||||||
 | |||||||
|
|
|
x0 x1 x3 x4 x5 x
Рис 17
Для получения единственного решения необходимо чтобы порядок многочлена Qm(x) совпадал с числом узлов интерполяции m=n, т. е. Имел вид Qn(x)=c0φ0(x)+c1φ1(x)+…+cnφn(x).
Для определения неизвестных постоянных коэффициентов с0, с1,…, сn используем условие интерполяции (3.3).
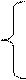с0φ0(x0)+c1φ1(x0)+…+cnφn(x0)=f(x0)
с0φ0(x1)+c1φ1(x1)+…+cnφn(x1)=f(x1) (3.4)
……………………………………..
с0φ0(xn)+c1φ1(xn)+…+cnφn(xn)=f(xn)
Система (3.4) – система линейных алгебраических уравнений относительно неизвестных с0, с1,…, сn. Данная система имеет единственное решение, если определитель системы не равен нулю:
φ0(x0) φ1(x0) … φn(x0)
φ0(x1) φ1(x1) … φn(x1) ≠0 (3.5)
………………………….
φ0(xn) φ1(xn) … φn(xn)
Система функций φ0(x), φ1(x), φ2(x),…, φn(x) должна быть линейно независимой.
Таким образом для решения задачи интерполирования необходимо выполнение следующих условий:
- Интерполяционный многочленQm(x) должен совпадать со значениями функции f(x) в узлах интерполяции;
- Порядок многочлена Qm(x) равен числу узлов интерполяции;
- Система функций φ0(х), φ1(х), φ2(х),…, φт(х) должна быть линейно независимой.
Решим систему (3.3) используя правило Крамера, представим многочлен Qn(x) в виде
Qn(x)=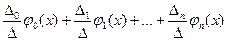 
, (3.6)
где Δ, Δi (i=0,…,n) - определители системы (3.4).
Раскрывая определители, окончательно преобразуем интерполяционный многочлен Qn(x):
Qn(x)=f(x0)Ф0(х)+f(x1)Ф1(x)+…+f(xn)Фn(x) (3.7)
где Фi(х) являются линейной комбинацией функций φ0(х), φ1(х),…, φn(x).
Учитывая интерполяционное условие (3.3), функции Фi(х) должны обладать следующим свойством:
Фi(xj)=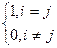 
(3.8)
|
|
|
