Интерполяционный многочлен Лагранжа

В качестве конечной совокупности функций φ₀(х), φ₁(х),…, φ_n(x) возьмем линейно независимую последовательность 1, x, x²,…, xⁿ. Введем обозначения Q_n(x)=L_n(x). Интерполяционный многочлен будет иметь вид:

L_n(x)=c₀+c₁x+…+c_nxⁿ. (3.9)

Используя интерполяционное условие (3.3), составим систему уравнений

с₀+с₁x₀+c₂x₀²+…+c_nx₀ⁿ=f(x₀)

с₀+с₁x₁+c₂x₁²+…+c_nx₁ⁿ=f(x₁) (3.10)

……………………………..

с₀+с₁x_n+c₂x_n²+…+c_nx_nⁿ=f(x_n)

Определителем данной системы является определитель Вандермонда:

1 x₀ x₀² … x₀ⁿ

Δ= 1 x₁ x₁² … x₁ⁿ = 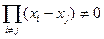(3.11)

………………..

1 x_n x_n² … x_nⁿ

и, следовательно, система имеет единственное решение. Функцию (3.8) из выражения (3.7) представим в виде

Ф_i(x)=A(x-x₀)(x-x₁)…(x-x_i-1)(x-x_i+1)…(x-x_n) (3.12)

где А- неизвестный постоянный коэффициент,

Х- промежуточная точка между узлами интерполяции.

Учитывая свойство (3.8), подставим х=х_i в (3.12) и определим коэффициент А:

A(x_i-x₀)(x_i-x₁)…(x_i-x_i-1)(x_i-x_i+1)…(x_i-x_n)=1,

A= 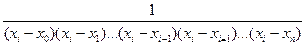, (3.13)

Интерполяционный многочлен (3.7) с учетом (3.12) и (3.13) запишем в виде:

(Q_n(x))L_n(x)= 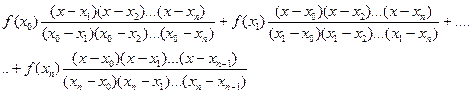(3.14)

L_n(x) называется интерполяционным многочленом Лагранжа.