Знакочередующиеся ряды представляют собой частный случай знакопеременных рядов, когда знаки членов «плюс» и «минус» поочередно меняются. Если считать все числа 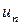 положительными, то знакочередующийся ряд в общем виде можно записать таким образом:
положительными, то знакочередующийся ряд в общем виде можно записать таким образом:
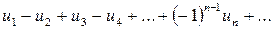 ,
, 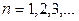 (11)
(11)
Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, и общий член ряда по модулю стремится к нулю.
Таким образом, для сходимости знакочередующегося ряда (11) достаточно выполнения двух условий:
1) 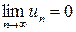 ;
;
2) 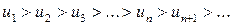 .
.
Следствия из теоремы Лейбница:
1) сумма сходящегося знакочередующегося ряда, записанного в форме (11), положительна и меньше его первого члена:
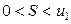 ; (12)
; (12)
2) если ряд (11) сходится по признаку Лейбница, то его остаток
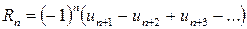
по модулю меньше своего первого члена: 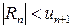 .
.
 2015-02-04
2015-02-04 1755
1755








