VI. п.4. Производные ФНП высших порядков

Пусть функция z = f (x, y) имеет в точке (x, y) и её окрестности непрерывные частные производные первого порядка 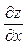и 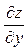. Так как 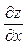и 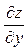являются функциями тех же аргументов x и y, то их можно дифференцировать по x и по y. При этом возможны следующие 4 варианта:

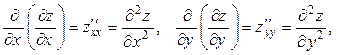
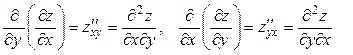
– эти частные производные называются частными производными второго порядка от функции z (x, y).

Частные производные 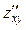и 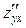называются смешанными частными производными второго порядка.

Пример. Дана ФНП 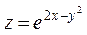. Вычислим все её частные производные второго порядка.

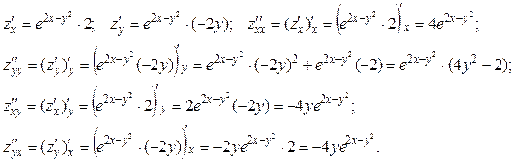
Основное свойство смешанных частных производных: если функция z = f (x, y) и её частные производные 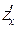, , 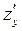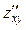и 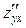определены и непрерывны в точке (x, y) и некоторой её окрестности, то в этой точке 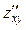= 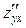, то есть смешанные частные производные при условии их непрерывности не зависят от порядка, в котором производится дифференцирование.