Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины обычно задается рядом распределения, который представляется в виде таблицы:
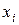 | 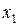 | 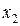 | … | 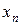 |
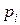 | 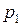 | 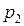 | … | 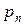 |
где в первой строке перечислены все возможные значения случайной величины, а во второй – соответствующие им вероятности 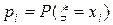 , удовлетворяющие соотношению
, удовлетворяющие соотношению 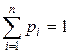 .
.
Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, т.е. в виде ломаной, соединяющей точки с координатами 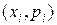 для
для 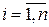 .
.
Математическим ожиданием или средним значением дискретнойслучайной величины 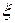 называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
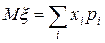 . (7)
. (7)
Дисперсией случайной величины 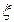 называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
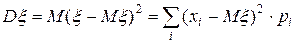 . (8)
. (8)
Для вычисления дисперсии на практике бывает удобнее использовать другую формулу, которую можно получить из формулы (8) с помощью простых преобразований:
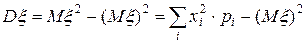 . (9)
. (9)
Средним квадратическим отклонением или стандартным отклонением случайной величины называется корень квадратный из ее дисперсии:
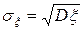 . (10)
. (10)
Задача 4. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,4. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения случайной величины 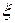 – числа очков, полученных стрелком за 3 выстрела, построить многоугольник распределения, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
– числа очков, полученных стрелком за 3 выстрела, построить многоугольник распределения, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Решение.
Случайная величина 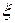 может принимать 4 значения:
может принимать 4 значения:
0 – если стрелок промахнулся 3 раза;
5 – если стрелок попал 1 раз при трех выстрелах;
10 – если стрелок попал 2 раза при трех выстрелах;
15 – если стрелок попал 3 раза.
Так как каждый выстрел можно рассматривать, как независимое испытание, в результате которого возможны только два исхода: попадание («успех») или промах («неудача»), то вероятности, соответствующие каждому значению случайной величины, можно найти по формуле Бернулли (5):
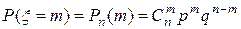 .
.
По условию задачи имеем: число испытаний 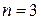 , вероятность успеха
, вероятность успеха 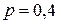 ,
, 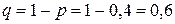 , значения
, значения 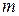 будут изменяться от 0 до 3. Т.о. имеем:
будут изменяться от 0 до 3. Т.о. имеем:
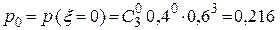 ,
,
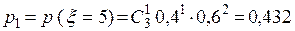 ,
,
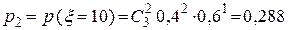 ,
,
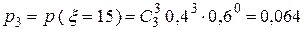 .о
.о
Следовательно, окончательно закон распределения случайной величины 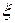 будет иметь вид:
будет иметь вид:
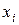 | ||||
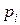 | 0,216 | 0,432 | 0,288 | 0,064 |
Построим многоугольник распределения. Для этого по оси абсцисс отложим возможные значения случайной величины, а по оси ординат – соответствующие им вероятности и соединяем точки (xi, pi) отрезками прямых. Полученная при этом ломаная линия и есть многоугольникраспределения вероятностей случайной величины 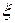 .
.
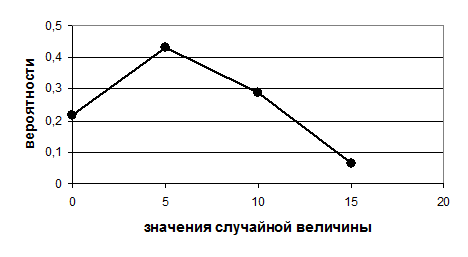 |
| Рис. 1. Многоугольник распределения вероятностей |
Рассчитаем числовые характеристики случайной величины 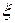 .
.
1. Математическое ожидание вычисляем по формуле (7)
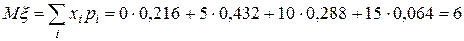 .
.
2. Дисперсия вычисляется по формуле (9):
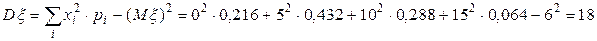 .
.
3. Среднее квадратическое отклонение
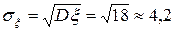 .
.
Ответ. Закон распределения случайной величины 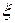 :
:
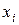 | ||||
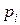 | 0,216 | 0,432 | 0,288 | 0,064 |
многоугольник распределения – на рисунке 1, 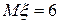 ,
, 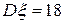 ,
, 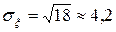 .
.
 2015-02-04
2015-02-04 3121
3121