Задача 2.1. Поезд массой 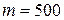 т движется равнозамедленно и в течение времени
т движется равнозамедленно и в течение времени 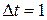 мин. уменьшает свою скорость от
мин. уменьшает свою скорость от 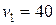 км/ч до
км/ч до 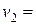
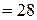 км/ч. Найти силу торможения.
км/ч. Найти силу торможения.
Решение. Запишем второй закон Ньютона в векторном виде
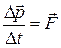 ,
,
откуда
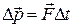
или
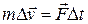 .
.
В проекции на направление движения последнее уравнение можно записать в виде
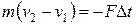 ,
,
откуда найдем
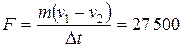 Н.
Н.
Задача 2.2. Брусок, масса которого 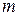 , тянут вдоль горизонтальной поверхности с силой
, тянут вдоль горизонтальной поверхности с силой 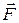 , приложенной под углом
, приложенной под углом 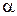 к горизонту. При этом брусок за время
к горизонту. При этом брусок за время 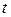 изменил свою скорость от
изменил свою скорость от 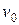 до
до 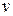 , двигаясь без отрыва от плоскости. Найти коэффициент трения
, двигаясь без отрыва от плоскости. Найти коэффициент трения 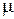 бруска о поверхность.
бруска о поверхность.
Решение. Сделаем чертеж, на котором изобразим силы, действующие на брусок (рис. 2.2). Запишем второй закон Ньютона в векторном виде
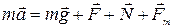 .
.
 Ускорение можно найти из кинематического уравнения
Ускорение можно найти из кинематического уравнения
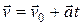 .
.
Исключив ускорение, имеем
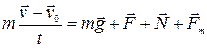 .
.
Запишем второй закон Ньютона в проекциях на оси 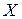 и
и 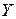 , учитывая, что
, учитывая, что 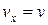 и
и 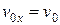 , поскольку движение происходит вдоль оси
, поскольку движение происходит вдоль оси 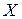 . Получим систему
. Получим систему
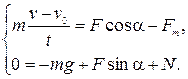
Поскольку 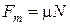 , имеем
, имеем
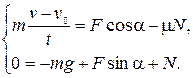
Из последней системы исключаем 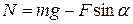 и окончательно находим
и окончательно находим
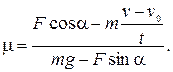
Задача 2.3. На платформе, масса которой равняется 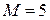 кг, лежит груз массой
кг, лежит груз массой 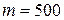 г. Коэффициент трения между платформой и грузом
г. Коэффициент трения между платформой и грузом 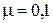 . Платформу тянут с силой
. Платформу тянут с силой 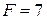 Н. Определить ускорения
Н. Определить ускорения 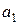 и
и 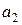 платформы и груза, если платформа движется по абсолютно гладкой поверхности.
платформы и груза, если платформа движется по абсолютно гладкой поверхности.
Решение. Поскольку в данной задаче рассматривается одномерное движение, то можно записать второй закон Ньютона для платформы и груза сразу в скалярном виде
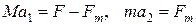 .
.
Поскольку 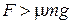 , груз скользит вдоль поверхности платформы и можно считать, что
, груз скользит вдоль поверхности платформы и можно считать, что 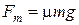 . Тогда
. Тогда
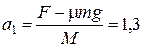 м/с2,
м/с2, 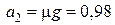 м/с2.
м/с2.
Задача 2.4. Камень, масса которого 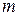 , падая с высоты
, падая с высоты 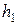 , попадает в снег и погружается в него на глубину
, попадает в снег и погружается в него на глубину 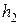 . Считая движение в воздухе и в снегу равнопеременным, найти силу сопротивления движению в снегу
. Считая движение в воздухе и в снегу равнопеременным, найти силу сопротивления движению в снегу 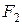 . Сила сопротивления в воздухе
. Сила сопротивления в воздухе 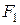 .
.
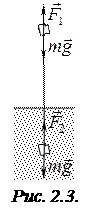 Решение. Сделаем схематический чертеж (рис. 2.3) и обозначим на нем силы, действующие на камень. Движение камня будем рассматривать на двух участках: в воздухе и в снегу. Запишем второй закон Ньютона и кинематические уравнения:
Решение. Сделаем схематический чертеж (рис. 2.3) и обозначим на нем силы, действующие на камень. Движение камня будем рассматривать на двух участках: в воздухе и в снегу. Запишем второй закон Ньютона и кинематические уравнения:
в воздухе: 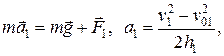
в снегу: 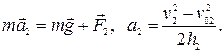
Учитывая, что 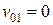 ,
, 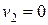 ,
, 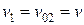 , имеем
, имеем
в воздухе: 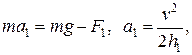 (1)
(1)
в снегу: 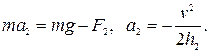 (2)
(2)
Исключим 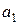 из уравнений (1) и
из уравнений (1) и 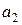 из уравнений (2), имеем
из уравнений (2), имеем
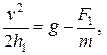
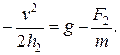
Отсюда, поделив первое уравнение на второе, после преобразований найдем
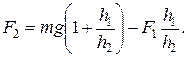
Задача 2.5. Канат лежит на столе таким образом, что его часть свисает со стола и начинает скользить лишь тогда, когда длина свисающей части равняется ¼ общей длины каната. Найти коэффициент трения 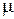 каната о стол.
каната о стол.
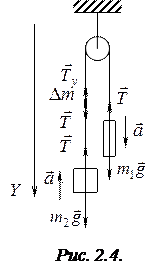 Решение. Обозначим силу тяжести, действующую на единицу длины каната, как
Решение. Обозначим силу тяжести, действующую на единицу длины каната, как 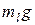 . Тогда сила тяжести свисающей части равняется
. Тогда сила тяжести свисающей части равняется 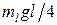 . Эта сила тяжести уравновешена силой трения
. Эта сила тяжести уравновешена силой трения 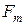 , действующей на ту часть каната, которая лежит на столе:
, действующей на ту часть каната, которая лежит на столе: 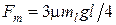 и канат начнет двигаться, когда сила тяжести части, которая свешивается, хотя бы немного превысит силу трения. Таким образом, в пределе
и канат начнет двигаться, когда сила тяжести части, которая свешивается, хотя бы немного превысит силу трения. Таким образом, в пределе 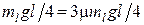 , откуда
, откуда 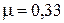 .
.
Задача 2.6. Два груза с массами 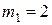 кг и
кг и 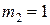 кг соединены нерастяжимой невесомой нитью, перекинутой через невесомый блок. Найти ускорение
кг соединены нерастяжимой невесомой нитью, перекинутой через невесомый блок. Найти ускорение 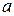 , с которым двигаются грузы, и силу натяжения нити
, с которым двигаются грузы, и силу натяжения нити 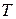 . Трением в оси блока пренебречь.
. Трением в оси блока пренебречь.
Решение. Воспользуемся тем, что нить нерастяжима. Выберем бесконечно малый элемент нити 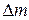 и запишем уравнение движения в проекции на ось
и запишем уравнение движения в проекции на ось 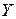 (рис. 2.4):
(рис. 2.4):
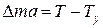 .
.
Поскольку 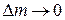 , имеем
, имеем 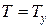 . Этим результатом можно пользоваться при дальнейшем решении задач: если нить невесома, то сила натяжения нити одинакова во всех ее точках.
. Этим результатом можно пользоваться при дальнейшем решении задач: если нить невесома, то сила натяжения нити одинакова во всех ее точках.
Покажем, что ускорение грузов также одинаково. Вследствие того, что нить нерастяжима, грузы проходят за одно и то же время одинаковый путь 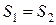
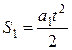 ,
, 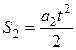 ,
,
т.е. 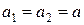 . Но направления векторов
. Но направления векторов 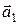 и
и 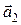 – противоположны.
– противоположны.
Запишем второй закон Ньютона для грузов в проекции на ось ОY:
для первого груза: 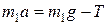 , (1)
, (1)
для второго груза: 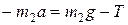 . (2)
. (2)
Вычитая (2) из (1), после преобразований имеем:
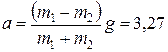 м/с2. (3)
м/с2. (3)
Для того, чтобы найти силу натяжения нити, (3) подставим в (1) и после преобразований будем иметь
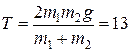 Н.
Н.
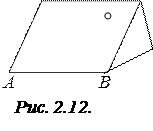 2.14. На наклонной плоскости лежит монета, которую удерживает сила трения (рис. 2.12). Как будет двигаться монета, если ей сообщить скорость в направлении, которое параллельно
2.14. На наклонной плоскости лежит монета, которую удерживает сила трения (рис. 2.12). Как будет двигаться монета, если ей сообщить скорость в направлении, которое параллельно 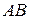 ? Будет ли ее движение прямолинейным?
? Будет ли ее движение прямолинейным?
– Не понимаю, почему монета не двигалась до сообщения скорости – п. 82.
– Что изменяется, когда монета приходит в движение – п. 99.
– Считаю, что монета будет двигаться прямолинейно – п. 110.
2.15. Через неподвижный блок перекинут длинный канат, на концах которого висят два гимнаста одинаковой массы. Гимнасты находятся на одинаковой высоте над землей и сначала неподвижны. Потом первый начинает подниматься со скоростью 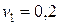 м/с относительно каната, а второй – со скоростью
м/с относительно каната, а второй – со скоростью 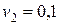 м/с относительно каната. Кто из них раньше достигнет блока? Канат и блок невесомы, трение в блоке отсутствует.
м/с относительно каната. Кто из них раньше достигнет блока? Канат и блок невесомы, трение в блоке отсутствует.
– Не знаю, с чего начинать – п. 65.
– Записал уравнения, но не могу их проанализировать – п. 146.
2.16. При быстром торможении трамвай, который имеет скорость 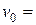 = 36 км/ч, пришел в движение «юзом». Какое расстояние
= 36 км/ч, пришел в движение «юзом». Какое расстояние 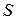 пройдет вагон с момента начала торможения до полной остановки? Коэффициент трения скольжения колес о рельсы
пройдет вагон с момента начала торможения до полной остановки? Коэффициент трения скольжения колес о рельсы 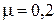 .
.
– Не понимаю, что означает «двигаться «юзом» – п. 68.
– Не знаю, как найти путь – п. 94.
– Не знаю, как найти ускорение – п. 131.
– Не знаю, как найти время движения – п. 144.
ОТВЕТЫ
 |
|
2.15. Достигнут блока одновременно.
2.16. 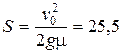 м.
м.
2.17. 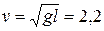 м/с.
м/с.
 2015-02-04
2015-02-04 1756
1756
