Периодический взнос на погашение кредита

Символ функции – PMT.

Таблица тип В — колонка № 6.

Временная оценка денежных потоков может поставить перед аналитиком проблему определения величины самого аннуитета, если известна его текущая стоимость, число взносов и ставка до­хода.

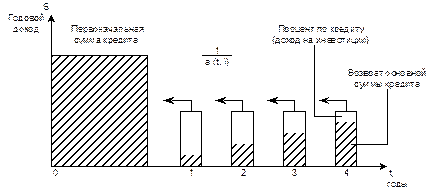
Рис. 4 Периодический взнос на погашение кредита.

Задача-алгоритм.

Какую сумму можно ежегодно снимать со счета в течение пяти лет, если первоначальный вклад равен 1500 тыс. руб., банк на­числяет ежегодно 14% и при условии, что снимаемые суммы будут одинаковы.

Решение:

1. Находим фактор взноса на погашение кредита при условии, что взносов будет 5, а ставка 14% (колонка №6). Фактор ра­вен 0,2913.

2. Рассчитаем величину аннуитета

1500 х PMT^5(14%) = 1500 х 0,2913 = 437 тыс. руб.

Таким образом, если положить на счет под 14% годовых 1500 тыс. руб., можно пять раз в конце года снять по 437 тыс. руб. Дополнительно полученные деньги в сумме (437 х 5)-1500 = 685 тыс. руб. являются результатом начисления процентов на уменьшающийся остаток вклада.

Функция «периодический взнос на погашение кредита» явля­ется обратной по отношению к функции «текущая стоимость ан­нуитета».

Аннуитет по определению может быть как поступлением, (т.е. входящим денежным потоком), так и платежом, (т.е. исходящим денежным потоком) по отношению к инвестору. Поэтому данная функция может использоваться в случае необходимости расчета величины равновеликого взноса в погашении кредита при задан­ном числе взносов и заданной процентной ставке. Такой кредит называют самоамортизирующимся.

Например, рассчитать величину ежегодного взноса в погаше­ние кредита в сумме 40000 тыс. руб., предоставленного на 15 лет под 20% годовых.

Решение:

1. Определим фактор периодического взноса на погашение кредита, если ставка – 20%, а число взносов – 15 (колонка №6) - 0,2139.

2. Рассчитаем величину взноса

40000 х PMT^15(20%) = 40000 х 0,2139 = 8555,3 тыс. руб.

Заемщик уплатил кредитору за 15 лет 128329,3 = (8555,3 х 15) тыс. руб., что превышает величину выданного кредита на 128329,3-40000 = 88329,3 тыс. руб. Разница является суммой процентов, уплаченных заемщиком за весь период кредитования, при условии, что основной долг по­стоянно уменьшается.