Координатный способ задания движения
В прямолинейной системе координат Oxyz вектор 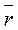 может быть представлен в виде
может быть представлен в виде
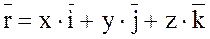 ,
,
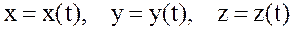 координаты точки М, определяющие закон ее движения в зависимости от времени t;
координаты точки М, определяющие закон ее движения в зависимости от времени t;
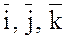 - нормированный базис Oxyz.
- нормированный базис Oxyz.
1. Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени:
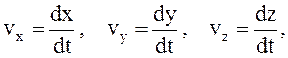
2. Проекции ускорения на оси координат равны первым производным от проекций скоростей точки или вторым производным от соответствующих координат точки по времени:
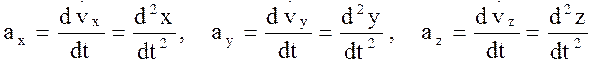
Величины (модули) скорости и ускорения в декартовой ортогональной системе координат определяют по формулам
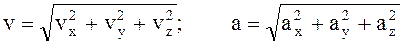 ,
,
а направления 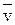 и
и 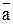 характеризуют их направляющие косинусы
характеризуют их направляющие косинусы
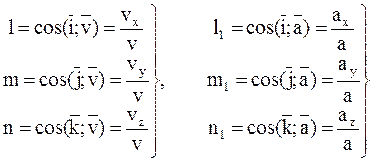 .
.
Задание движения в естественных осях
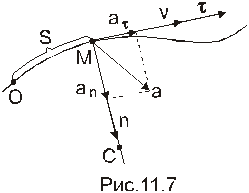
Предельное положение прямой, проходящей через точки М и М1 траектории L точки М, когда М1 стремится к М, определяет касательную к этой кривой в точке М. Обозначим 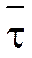 - единичный направляющий вектор касательной к L в точке М.
- единичный направляющий вектор касательной к L в точке М.
Соприкасающаяся плоскость в точке М кривой L определяется как предельное положение плоскости, содержащей в себе касательную в точке М кривой и любую точку М1 на ней, когда М1 стремится к М.
Нормаль 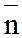 к кривой в точке М, лежащую в соприкасающейся плоскости, называют главной нормалью к кривой в т.М. Нормаль
к кривой в точке М, лежащую в соприкасающейся плоскости, называют главной нормалью к кривой в т.М. Нормаль 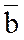 к кривой, перпендикулярную соприкасающейся плоскости, называют бинормалью.
к кривой, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Прямоугольную систему взаимно ортогональных осей, направленных по 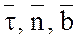 называют естественными осями кривой L. Направление вектора скорости принимают за положительное направление касательной
называют естественными осями кривой L. Направление вектора скорости принимают за положительное направление касательной 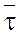 .
.
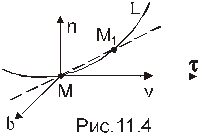

 Положительное направление главной нормали считают в сторону вогнутости кривой, а бинормаль направляют так, чтобы получившаяся система осей
Положительное направление главной нормали считают в сторону вогнутости кривой, а бинормаль направляют так, чтобы получившаяся система осей  являлась правой.
являлась правой.
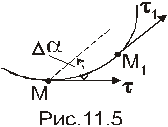 Кривизной «k» кривой L в точке М называют предел
Кривизной «k» кривой L в точке М называют предел
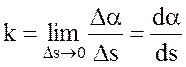 .
.
Радиусом кривизны «r» кривой L в точке М называют величину обратную ее кривизне в этой точке
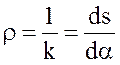 .
.
Так, например, дуга окружности длиной s, опирающаяся на центральный угол 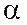 :
: 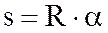 ,
,
где R – радиус окружности, то радиус кривизны для окружности 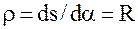
Ускорение точки можно разложить на тангенциальное 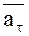 , направленное по касательной к траектории и характеризующее изменение величины скорости, и нормальное
, направленное по касательной к траектории и характеризующее изменение величины скорости, и нормальное 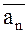 , направленное по главной нормали к центру кривизны траектории и определяющее изменение направления
, направленное по главной нормали к центру кривизны траектории и определяющее изменение направления 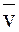 .
.
 Так как в естественных осях траектории скорость может быть представлена в виде
Так как в естественных осях траектории скорость может быть представлена в виде 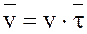 , то, дифференцируя это соотношение по времени, получим ускорение:
, то, дифференцируя это соотношение по времени, получим ускорение:
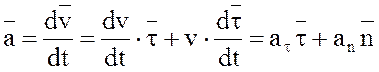 , Касательное ускорение (проекция ускорения точки на касательную) равно первой производной от величины скорости от времени:
, Касательное ускорение (проекция ускорения точки на касательную) равно первой производной от величины скорости от времени:
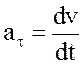
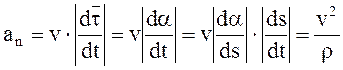
Абсолютная величина 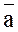 может быть определена по формуле
может быть определена по формуле
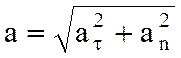 .
.
Задача. По заданным уравнениям движения точки
x = 2t (см), 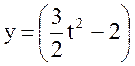 (см)
(см)
определить ее траекторию, положение, скорость, ускорение, касательное и нормальное ускорения, радиус кривизны траектории в заданное время t1 = 2c.
Решение.
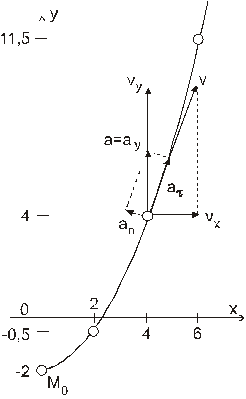 1.Уравнение траектории получим, исключив из уравнений движения время:
1.Уравнение траектории получим, исключив из уравнений движения время: 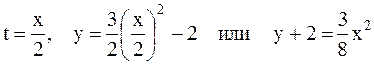 - парабола с вершиной в точке (0,-2).
- парабола с вершиной в точке (0,-2).
Построим траекторию по точкам: 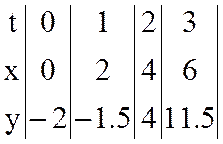
2.Величина скорости точки 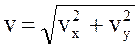 ;
; 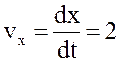 см/с;
см/с; 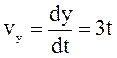 ; при t1=2с, vx=2 см/с vy=6см/с;
; при t1=2с, vx=2 см/с vy=6см/с; 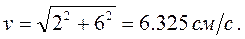
3. Величина ускорения точки 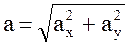 ;
; 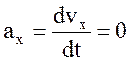 ;
; 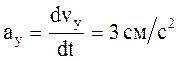 ;
; 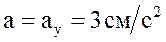 .
.
4.Касательное ускорение 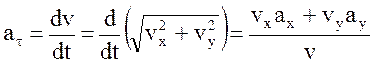 ; при t1 = 2с
; при t1 = 2с 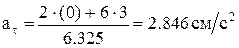 .
.
при t1 = 2c: 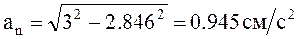 .
.
6.Радиус кривизны траектории 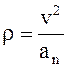
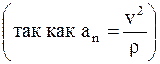 ; при t1 = 2c
; при t1 = 2c
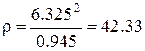 см.
см.
Твердые тела можно рассматривать как совокупность точек, расстояния между которыми в процессе их перемещения остаются неизменными. Угол между пересекающимися прямыми, связанными с телом, сохраняется без изменения, а параллельные прямые остаются параллельными при его движении. Положение точек твердого тела полностью определено, если известно положение трех его точек, не лежащих на одной прямой.
1. Простейшие движения твердого тела
К простейшим относятся поступательное и вращательное движение тела вокруг неподвижной оси.
1.1. Поступательное движение. При поступательном движении любой отрезок прямой (например, отрезок АВ), проведенный в твердом теле, остается параллельным самому себе.
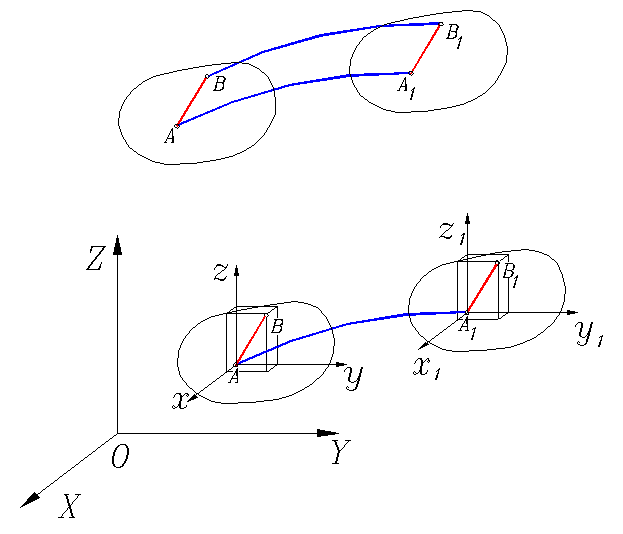
Выберем подвижную систему отсчета Axyz, оси которой связаны с данным телом и передвигаются вместе с ним.
Т. к. при поступательном движении оси координат остаются параллельными своему начальному направлению, координаты любой точки (например т. В) твердого тела в подвижной системе отсчета остаются постоянными, а ее движение тождественно движению т. А.
Следовательно, траектории движения всех точек одинаковы. Одинаковыми по модулю и направлению будут также скорости и ускорения твердого тела при его поступательном движении.
 2014-02-09
2014-02-09 1217
1217

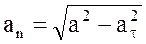 ;
;






