Критерий взвешенного среднего

4) Критерий взвешенного среднего (аддитивной свертки):

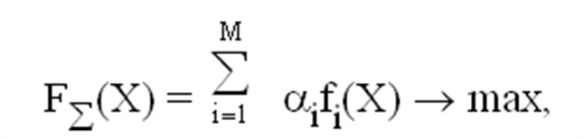
где αi - коэффициент относительной значимости i-гo показателя в интегральной оценке полезности альтернативы, каждый αi принимает значение от 0 до 1, сумма всех коэффициентов αi равна 1.

Данный способ выбора альтернативы является одним из наиболее распространенных. Выбор осуществляется по наилучшему значению комплексного показателя FΣ, которое представляет собой интегральную оценку полезности альтернативы.

Вернемся к примеру с двумя альтернативами X1 и Х2 в предыдущем пункте. Пусть эксперты совместно с ЛПР определили относительную важность показателей стоимости и показателя временных затрат. Положим, что для ЛПР значительно более важным является сокращение временных затрат на выполнение мероприятия, и он согласен сократить эти затраты за счет увеличения стоимости. Тогда могут быть выбраны такие весовые коэффициенты: α1 = 0.2, α2= 0.8 (заметим, что в сумме они дают единицу). Разница между коэффициентами покажет, насколько один из показателей важнее другого. С учетом этого имеем следующие результаты:

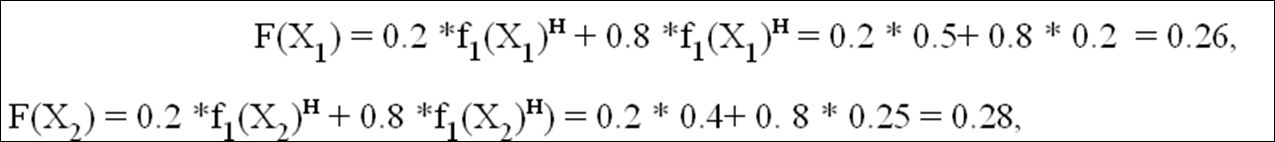
и по критерию минимизации затрат необходимо выбрать альтернативу X1 (вспомним, что в случае, когда показатели были равнозначны и мы применяли среднее арифметическое, лучшей была признана альтернатива Х2.