Движение осуществляется в течение абсолютного времени

В МСС изучаются индивидуальные или субстанциональные [2] объемы среды. Условимся называть их частицами, и будем рассматривать их как отдельные термодинамические системы. Таким образом, предполагается, что для такой частицы справедливы все выводы термодинамики, которые получены для равновесных систем. Это предположение носит название гипотезы о локальном термодинамическом равновесии.

Напомним основные положения термодинамики.

Если в системе нет изменений параметров, и отсутствуют потоки, то говорят, что система находится в термодинамическом равновесии.

Нулевое начало термодинамики. Две термодинамические системы находящееся в термодинамическом равновесии с третьей, находятся в термодинамическом равновесии между собой (закон термодинамической транзитивности). Функцию состояния системы Т называют эмпирической температурой.

Первое начало термодинамики - закон сохранения энергии в частице. Тепло подводимое к частице идет на повышения ее внутренней энергии и работу внутренних сил.

Второе начало термодинамики – закон изменения энтропии. Энтропия (мера хаоса) изолированной системы не уменьшается. В частности это означает, что тепло передается от нагретого к холодному, а так же в другой формулировке - невозможность существования вечного двигателя второго рода.

В настоящее время МСС принято делить на две области:

механику жидкости и газа; механику твёрдых деформируемых тел.

Механика жидкости и газа включает в себя:

Газовую динамику (механику сжимаемых сред) и

Гидромеханику (механику несжимаемых сред):

· механики идеальной жидкости;

· механики вязкой ньютоновской жидкости;

· механики аномально вязкой неньютоновской жидкости;

· механики турбулентных течений.

Механика деформируемых твёрдых тел изучает:

· теорию упругости;

· теорию пластичности;

· теорию ползучести;

· теорию разрушения;

· механику сыпучих тел.

Как мы увидим в дальнейшем, математические модели МСС приводят к необходимости решения систем сложных нелинейных дифференциальных уравнений. При их решении приходится сталкиваться с очень большими математическими трудностями, а точные аналитические решения получены только для простых задач. Поэтому, исторически сложилось разделение МСС на теоретическую МСС и практическую – гидравли ку (техническую гидрогазодинамику). Задачи первой - разработка математических моделей МСС и методов их решения. Задачей второй – разработка эмпирических (использующих экспериментальные данные) и полуэмпирических моделей для расчета конкретных механизмов, технических устройств и сооружений. В последние время с развитием численных методов решения, и ростом мощности вычислительной техники грань между этими частями МСС стирается.

1.2. Плотность распределения характеристик в сплошной среде.

Для определения характеристик сплошной среды мы можем использовать предельные переходы. Например, плотность вещества в точке пространства с координатами 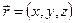определяется зависимостью:

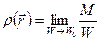, (1.1.4)

где 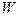- объём, занятый веществом; 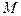- масса этого объёма; 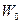- наименьший объём, окружающий точку с координатами 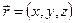, содержащий достаточно представительное число молекул. Если 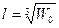- характерная длина 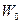подчиняется условию сплошности (1.1.1), то 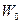- можно практически считать равным 0, а выражение для плотности записать в виде:

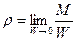. (1.1.5)

Аналогичные рассуждения можно использовать и при определении скорости движения жидкости или газа в рамках модели сплошной среды:

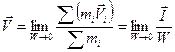. (1.1.6)

где 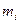- масса, 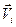- скорость молекулы, атома или другой частицы сплошной среды, а суммирование проводится по всем частицам, в объеме .

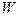Плотность распределения той или иной характеристики сплошной среды в пространстве или на поверхности это количество этой характеристики, приходящееся на единицу объёма или площади поверхности. Иначе говоря, это функция координат и времени 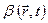, которая, будучи умножена на элементарный объём 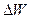(или элементарную площадку 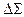), отразит общее количественно рассматриваемой характеристики этого объёма (площадки). При этом неявно предполагается, что 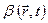внутри объема постоянна 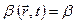, а элементарные объем 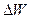и площадка 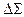малы. Пусть кинетическая энергия элементарного объёма 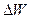, имеющего массу 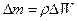и скорость 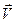, равна:

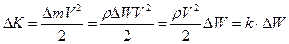. (1.2.1)

Здесь 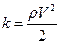- плотность распределения кинетической энергии.

Если рассматриваемая величина - вектор, то плотность ее распределения также вектор. Например, количество движения этого же элементарного объёма 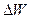равно:

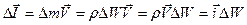. (1.2.2)

Здесь 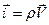- плотность распределения количества движения.

Пусть 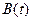- общее количество какой-либо характеристики объёма сплошной среды 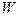в момент времени t, а 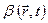- плотность распределения этой характеристики. Разобъем объём 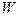на элементарные объёмы 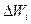, где i - порядковый номер элементарного объёма. Количество рассматриваемой гидромеханической характеристики в пределах i - го элементарного объёма равно 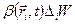, где 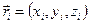- координаты любой внутренней точки объёма 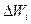. Подсчитаем общее количество характеристики, относящееся к объёму 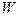, используя принцип суперпозиции:

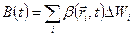.(1.2.3)

Рассматривая элементарный объём как бесконечно малую величину, можно записать

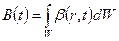. (1.2.4)

Плотность сплошной среды 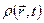можно назвать плотностью распределения массы (в пространстве), при этом массу М объёма 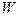можно представить в виде:

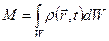. (1.2.5)

Введем аналогичным образом векторную величину 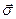– напряжение, как плотность распределения силы 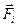по поверхности:

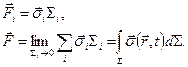. (1.2.6)

Проекцию напряжения на вектор единичной внешней нормали к поверхности будем называть 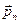- нормальным напряжением, проекцию на касательную плоскость 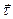– касательным напряжением.

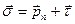. (1.2.7)

Под давлением 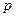будем понимать

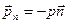. (1.2.8)

Сила в системе СИ измеряется в Н – ньютонах, а давление в Па. Таким образом, давление есть величина нормальной силы отнесенной к поверхности – плотность распределения нормальной силы по поверхности.