Безнапорные потоки. Струи

К безнапорным потокам обычно относят: течение в неполностью заполненном трубопроводе, течения в руслах, каналах, лодках, а также струйные течения. Особенностью таких течений является постоянство давления в области течения. Для их расчета также может быть использована формула Дарси-Вейсбаха (3.5.5), понятия гидравлического радиуса и смоченного периметра (рис.3.7) и упрощенное уравнение Бернулли:

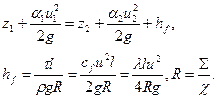(3.6.1)

Здесь 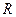- гидравлический радиус, 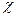- смоченный периметр. Используя понятие гидравлического уклона 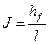можно записать зависимость для средней скорости потока:

(3.6.2)

Коэффициент 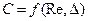называется коэффициентом Шези. 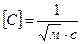. Для его вычисления можно использовать формулу Павловского:

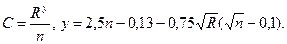(3.6.3)

Здесь 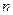- параметр шероховатости зависящий от материала русла ().

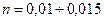Рассмотрим струйные установившиеся потоки, возникающие при истечении из резервуаров в свободную атмосферу. Отверстия и устройства (насадки, сопла), через которые осуществляется истечение, могут быть весьма разнообразными, поэтому единого метода их расчета не существует[9]. Образующиеся при этом струи так же имеют различную форму. Ограничимся рассмотрением простейших случаев.

Определим гидравлический напор истечения 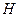как расстояние от центра отверстия истечения до свободной поверхности. Если диаметр отверстия 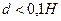, напор истечения постоянен, отверстие имеет острые кромки или толщина стенки резервуара много меньше его диаметра, то говорят что имеет место истечение через малое отверстие в тонкой стенке (рис.3.10).

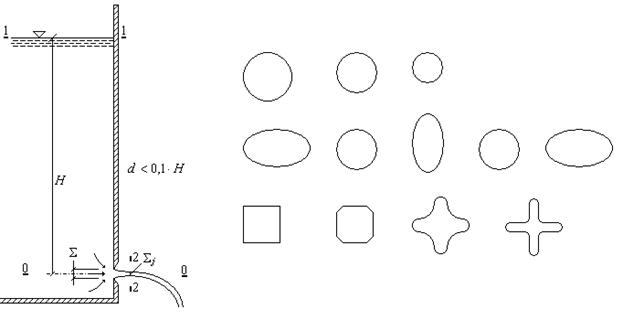
Рис.3.12.

Истечение через малое отверстие в атмосферу.

Линии тока жидкости, перед истечением, искривляются и направлены к центру отверстия. Это приводит к эффекту сужения (сжатия) струи, когда площадь сечения струи 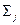меньше площади отверстия 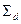. Обычно такое живое сечение струи формируется на некотором расстоянии 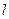от отверстия и называется сжатым, (для круглого отверстия 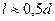). Отношение 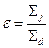называется коэффициентом сжатия струи. В случае некруглого отверстия иссечения форма живого сечения струи может претерпевать периодические изменения, показанные в левой части рисунка. Данное явление носит название – инверсия струи, и вызвано взаимодействием сил инерции и поверхностного натяжения.

Определим основные характеристики истечения, для этого запишим уравнение Бернулли для сечений 1-1 и 2-2.

.

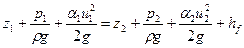В нашем случае: 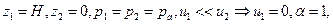тогда:

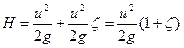, (3.6.4)

Здесь 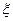- коэффициент местного сопротивления отверстия.

Скорость истечения в сжатом сечении и расход можно определить по формулам:

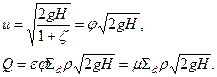(3.6.5)

Где 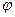- коэффициент скорости отверстия, 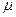- коэффициент расхода отверстия, для каждого типа истечения они определяются эмпирически. Для нашего случая их зависимость от 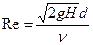- числа Рейнольдса истечения приведены на рис.3.10.

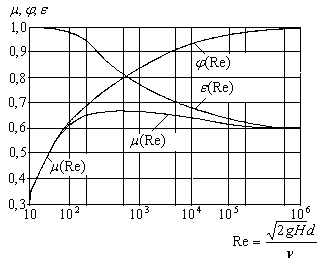
Рис.3.13.

Коэффициенты истечения для малых круглых отверстий.