Пусть на отрезке[ a, b ] задана непрерывная знакопостоянная функция y=f(x). Объемы тела вращения, образованного вращением вокруг оси Ох (или оси Оу) криволинейной трапеции, ограниченной кривой y=f(x) (f(x) 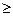 0) и прямыми у=0, х=а, х=b, вычисляются соответственно по формулам:
0) и прямыми у=0, х=а, х=b, вычисляются соответственно по формулам:
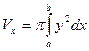 , ( 19 )
, ( 19 )
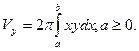 (20)
(20)
Если тело образуется при вращении вокруг оси Оу криволинейной трапеции, ограниченной кривой 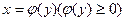 и прямыми x=0, y=c, y=d, то объем тела вращения равен
и прямыми x=0, y=c, y=d, то объем тела вращения равен
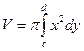 . (21)
. (21)
Пример. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями 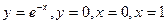 вокруг оси Ох.
вокруг оси Ох.
По формуле (19) искомый объем
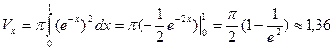 (ед.2)
(ед.2)
Пример. Пусть в плоскости xOy рассматривается линия y=cosx на отрезке 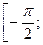
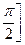 .
.
 |
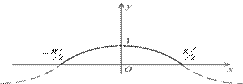 Эта линия вращается в пространстве вокруг оси
Эта линия вращается в пространстве вокруг оси 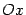 , и полученная поверхность вращения ограничивает некоторое тело вращения (см. рис.). Найдём объём
, и полученная поверхность вращения ограничивает некоторое тело вращения (см. рис.). Найдём объём 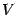 этого тела вращения.
этого тела вращения. Согласно формуле, получаем:
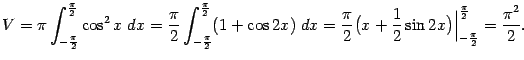
 2015-02-04
2015-02-04 1539
1539
