Тригонометрические функции, их свойства и графики

Функция синус y = sin(x).

Изобразим график функции синус, его называют "синусоида".

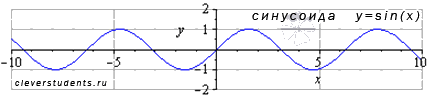
Свойства функции синус y = sinx:

1. Областью определения: .
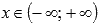2. Область значений:
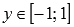
3. Наименьший положительный период функции синуса равен .
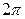4. Функция обращается в ноль при 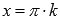, где 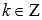, Z – множество целых чисел.
5. Функция синус - нечетная.
6. Функция убывает при ,
   
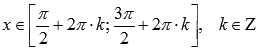   возрастает при .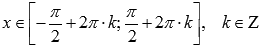
7. Функция синус имеет локальные максимумы в точках ,
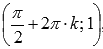   локальные минимумы в точках .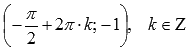
8. Функция y = sinx вогнутая при ,
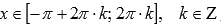   выпуклая при .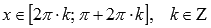
9. Координаты точек перегиба .
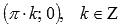10. Асимптот нет.

Функция косинус y = cos(x).

График функции косинус (его называют "косинусоида") имеет вид:

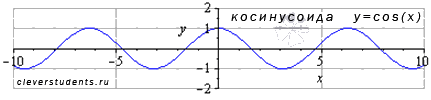
Свойства функции косинус y = cosx:

1. Область определения функции косинус: .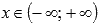

2. Область значений: .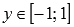

3. Наименьший положительный период функции косинус равен .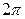

4. Функция обращается в ноль при 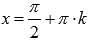, где 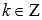, Z – множество целых чисел.

5. Функция косинус - четная.

6. Функция убывает при ,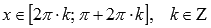
возрастает при .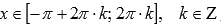

7. Функция y = cosx имеет локальные максимумы в точках ,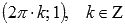
локальные минимумы в точках .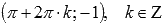

8. Функция вогнутая при ,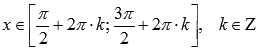
выпуклая при .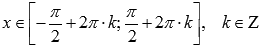

9. Координаты точек перегиба .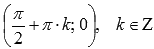

10. Асимптот нет.

Функция тангенс y = tg(x).

График функции тангенс (его называют "тангенсоида") имеет вид:

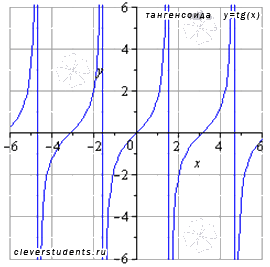
Свойства функции тангенс y = tgx:

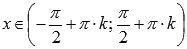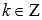1. Область определения функции тангенс: , где , Z – множество целых чисел.

2. Область значений функции тангенс: .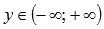

3. Наименьший положительный период функции тангенс равен .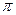

4. Функция обращается в ноль при 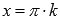, где 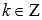, Z – множество целых чисел.

5. Функция тангенс - нечетная.

6. Функция возрастает при .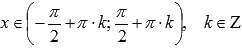

7. Функция вогнутая при ,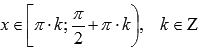

выпуклая при .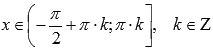

8. Координаты точек перегиба .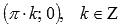

9. Наклонных и горизонтальных асимптот нет.

Функция котангенс y = ctg(x).

Изобразим график функции котангенс (его называют "котангенсоида"):

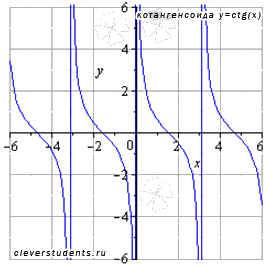
Свойства функции котангенс y = ctgx:

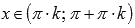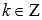1. Область определения: , где , Z – множество целых чисел.

2. Область значений: .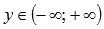

3. Наименьший положительный период функции котангенс равен .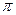

4. Функция обращается в ноль при 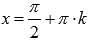, где 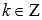, Z – множество целых чисел.

5. Функция нечетная.

6. Функция котангенс убывает при .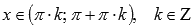

7. Функция котангенс вогнутая при ,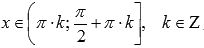
выпуклая при .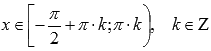

8. Координаты точек перегиба .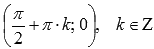

9. Наклонных и горизонтальных асимптот нет.