При неравномерном движении полосы имеют место инерционные усилия, оказывающие влияние на взаимодействие сил в зеве валков. Так как даже в реверсивных станах при скоростях 2,5—3 м/сек эти силы инерции незначительны [95] по сравнению с вертикальным давлением металла на валок, то их можно не учитывать. Силы инерции имеют значительную величину при захвате.
Рассмотрим случай (фиг. 96) захвата валками полосы, имеющей скорость 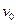 , меньшую скорости прокатки
, меньшую скорости прокатки 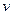 при установившемся движении. Обычно в практике
при установившемся движении. Обычно в практике 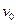 <
< 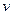 , кроме непрерывных станов, на которых
, кроме непрерывных станов, на которых 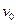 =
= 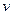 .
.
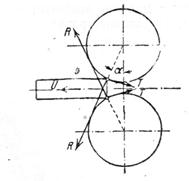
Фиг. 96. Действие сил на полосу в момент захвата
Когда 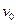 <
< 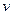 , вся масса полосы за период захвата получает значительное ускорение и ее скорость увеличивается от
, вся масса полосы за период захвата получает значительное ускорение и ее скорость увеличивается от 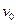 до
до 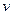 .
.
Обозначая ускорение полосы через е, подсчитаем силу инерции, противодействующую захвату:
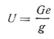
Пренебрегая силами трения в проводках, на рольгангах и т. д., можем составить уравнения равновесия сил, имея в виду, что со стороны валков к полосе приложены две нормальные силы  и две тангенциальные силы Т.
и две тангенциальные силы Т.
Проектируя эти силы на направление движения полосы, получаем:
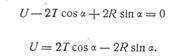 (117)
(117)
Пренебрегая силами трения в подшипниках и выражая равнодействующую касательных усилий Т через приводной момент двигателя М пр обоих валков, получаем:
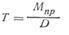 (118)
(118)
Если обозначить коэффициент трения между валком и прокатываемым металлом через 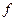 , уравнение (117) примет вид:
, уравнение (117) примет вид:
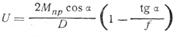 (119)
(119)
При том же М пр сила инерции увеличивается с уменьшением угла захвата 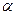 ; максимального значения эта сила достигает при
; максимального значения эта сила достигает при 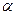 =0,
=0,
когда:
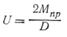
При 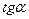 >
> 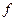 сила инерции становится отрицательной и захват полосы валками невозможен.
сила инерции становится отрицательной и захват полосы валками невозможен.
На каждый валок и его подшипники боковое давление действует в сторону, противоположную направлению прокатки, а сила Х= 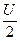 .
.
 2015-02-14
2015-02-14 466
466








