2015-02-14
514
Для сравнения темпов роста денежных средств по разным ставкам достаточно сопоставить соответствующие множители наращения. При одинаковых значениях ставок величины множителей существенно зависят от продолжительности ФО t.
Сравнивая темпы роста денежных средств по простой процентной и простой учетной ставкам, сопоставляют множители наращения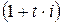 
и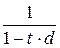 
, полагая в них 
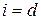[2]. Тогда в соответствии со свойствами прямой линии и гиперболы возможны два варианта соотношений (см. рис. 2.4):
– если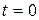 
, то 
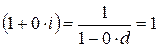– значения наращенных сумм 
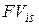и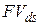 
совпадают и равны современной стоимости PV;
– если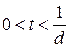 
, то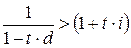 
– больший процентный доход кредитору даст простая учетная ставка d.
На рис. 2.4 видно, что линия 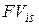наращения по простой процентной ставке является касательной к линии 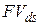наращения по простой учетной ставке.
Сравнивая темпы роста денежных средств по простой и сложной процентным ставкам, сопоставляют множители наращения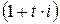 
и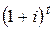 
. Тогда в соответствии со свойствами прямой линии и показательной функции возможны четыре варианта соотношений (рис. 2.5):
|
|
|
– 
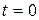если , то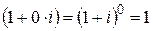 
– значения наращенных сумм 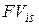и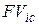 
совпадают и равны современной стоимости PV;
– если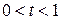 
, то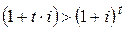 
– при продолжительности ФО менее одного периода начисления процентов (например, года) больший процентный доход кредитору дает простая ставка;
– если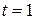 
, то 
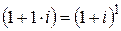– при продолжительности ФО, равной одному периоду начисления процентов обе ставки дают кредитору одинаковый процентный доход;
– если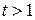 
, то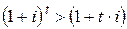 
– при продолжительности ФО более одного периода начисления процентов больший процентный доход кредитору дает сложная ставка.
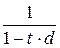Сравнивая темпы роста денежных средств по простой и сложной учетным ставкам, сопоставляют множители наращения и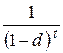 
(рис. 2.6):
– если 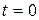, то 
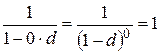– значения наращенных сумм 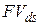и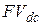 
совпадают и равны современной стоимости PV;
– если 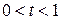, то 
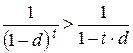– при продолжительности ФО менее одного периода начисления процентов больший процентный доход кредитору дает сложная ставка;
– если 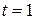, то 
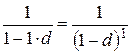– при продолжительности ФО, равной одному периоду начисления процентов обе ставки дают кредитору одинаковый процентный доход;
– если 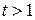, то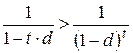 
– при продолжительности ФО более одного периода начисления процентов больший процентный доход кредитору дает простая ставка.
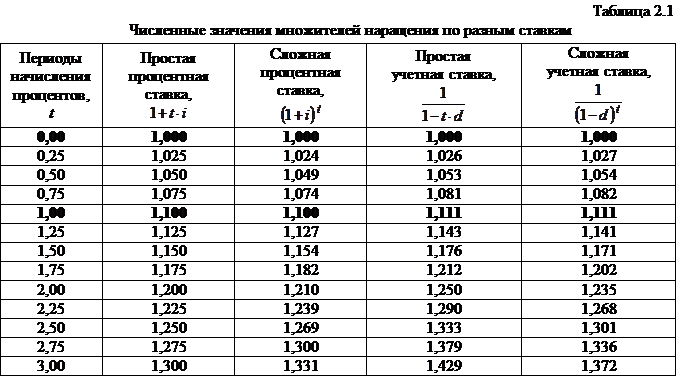
Для иллюстрации сравнительных характеристик темпов роста денежных средств по разным ставкам в табл. 2.1 приведены численные значения множителей наращения при заданной ставке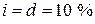 
для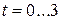 
периодов начисления процентов, а на рис. 2.7 – графики наращения. Таблица показывает, что при прочих равных условиях наименьший процентный доход кредитору при 
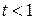дает сложная процентная ставка, а наибольший – сложная учетная ставка, тогда как при 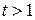наименьший процентный доход дает простая процентная ставка, а наибольший – простая учетная ставка. При 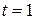учетные ставки дают больший процентный доход, чем процентные ставки.
|
|
|
Пример 2.4. Клиент получил финансовый кредит 40 000 рублей на срок 7 месяцев. Ставка наращения – 12% годовых. Определить сумму долга вместе с процентами для четырех основных ставок (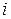
, 
, 
, 
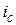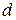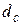). Оценить, по какой ставке наращение происходит быстрее.
