2015-02-14
494
Иногда при составлении финансово-кредитных соглашений оговаривают эквивалентность ставок.
Эквивалентными называют такие ставки, которые по истечении заданного периода времени дают одинаковые денежные суммы.
Для установления эквивалентности между простыми процентной i и учетной d ставками необходимо приравнять наращенные суммы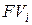 
и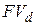 
, определяемые формулами (2.2) и (2.17), и выразить эквивалентную ставку через исходную ставку. Пусть в финансовом соглашении исходно была задана простая учетная ставка d, а затем было решено заменить ее эквивалентной простой процентной ставкой i. Тогда необходимо выразить ставку i через ставку d:
 ;
| ||
 ;
| ||
 ;
| ||
 .
|
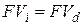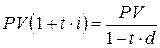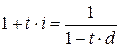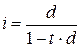Если бы ситуация была иной, и исходной была бы простая процентная ставка, а эквивалентной – простая учетная, то формула имела бы вид
 .
|
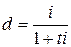Аналогично можно установить эквивалентность между всеми ставками. Выполненные преобразования показывают, что для получения формул эквивалентности ставок достаточно попарно приравнять соответствующие множители наращения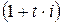 
, 
, 
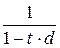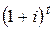и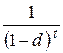 
[2, 3, 5, 6]. Приравнивая данные формулы, опуская алгебраические преобразования и вводя обозначение 
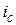для сложной процентной ставки и 
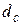для сложной учетной ставки, получаем необходимые расчетные формулы эквивалентных ставок (табл. 2.3).
|
|
|
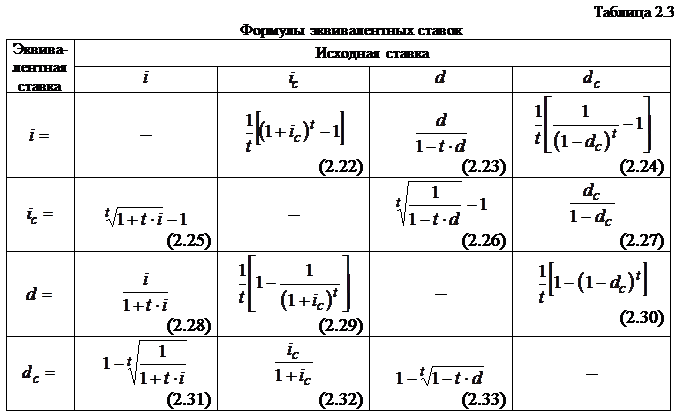
Если продолжительность ФО задана числом дней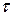 
, а расчеты выполняют при разных значениях временных баз (
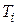– для ставки i, 
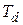– для ставки d), то, например, формулы (2.23) и (2.28) примут вид:
 ;
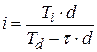| (2.34) | |
 .
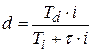| (2.35) |
Тогда пр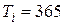и 
и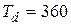 
по формулам (2.34) и (2.35) получим:
 ;  .
|
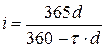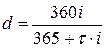Пример 2.6. Финансовый кредит на сумму 60 000 рублей выдан на срок 14 месяцев. Сложная процентная ставка 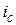27% годовых. Определить три эквивалентные ставки (
, 
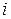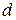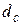, ) и по всем четырем ставкам построить графики наращения с интервалом 2 месяца. При расчете эквивалентных ставок в долях единицы округление выполнять до 5-го знака в дробной части.
