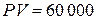2015-02-14
373
руб.;
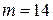мес.;
.
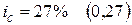Продолжительность данной ФО задана в месяцах, поэтому в расчетных формулах выполняем подстановку (1.7):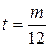 
. Для расчета эквивалентных ставок при заданной сложной процентной ставке 
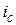используем формулы (2.22), (2.29), (2.32) из табл. 2.3:
;
;
.
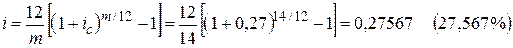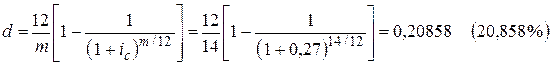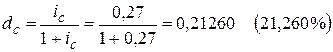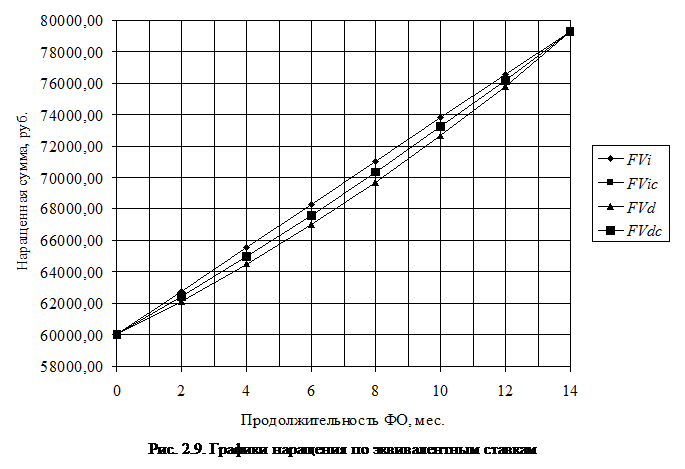
Согласно определению, эквивалентные ставки по истечении заданного периода времени дают одинаковые денежные суммы, следовательно, все четыре графика наращения выходят из одной точки и по истечении 14-ти месяцев сходятся в одной точке. Результаты расчета представим в табл. 2.4, графики наращения – на рис. 2.9.
Таблица 2.4
| Продолжительность ФО, m |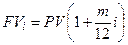 
| 
| 
| 
|
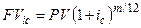
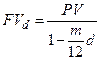
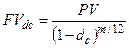
| 60 000,00 | 60 000,00 | 60 000,00 | 60 000,00 | |
| 62 756,70 | 62 438,42 | 62 160,92 | 62 438,44 | |
| 65 513,40 | 64 975,93 | 64 483,31 | 64 975,97 | |
| 68 270,10 | 67 616,57 | 66 985,97 | 67 616,63 | |
| 71 026,80 | 70 364,52 | 69 690,73 | 70 364,61 | |
| 73 783,50 | 73 224,15 | 72 623,11 | 73 224,27 | |
| 76 540,20 | 76 200,00 | 75 813,10 | 76 200,15 | |
| 79 296,90 | 79 296,79 | 79 296,20 | 79 296,97 |
Полученные данные показывают, что наращение по сложным эквивалентным ставкам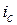 
и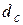 
даёт одинаковые результаты, поэтому фактически на рис. 2.9 представлены три графика наращения. График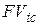и 
и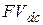 
совпадают.
|
|
|
2.10. Наращение и реинвестирование денежных средств с использованием
плавающих ставок
Финансовое соглашение может предусматривать изменяющиеся во времени ставки, называемые плавающими (floating interest rate) [2]. Плавающие ставки позволяют уменьшить влияние инфляции на результаты ФО. В этом случае устанавливают базовую процентную ставку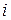 
, величину надбавки или маржу (margin), которая может быть как постоянной 
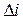, так и переменной 
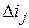, а также продолжительность периодов времени 
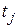, в каждом из которых ставка будет оставаться неизменной. Тогда в течение периода 
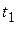величина процентной ставки составит 
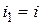. За период 
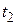величина ставки составит 
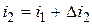. При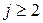 
за очередной j -й период величина ставки составит 
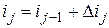. В зависимости от условий конкретной ФО ставка 
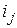может быть простой или сложной.
Тогда при использовании простой процентной ставки за каждый j -й период на сумму PV в соответствии с формулой (2.1) будут начислены проценты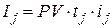 
, а за период времени, соответствующий продолжительности ФО и состоящий из k периодов, процентный доход I составит
 .
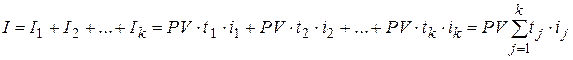| (2.36) |
С учетом формул (2.2) и (2.36) можно выразить наращенную сумму FV:
 .
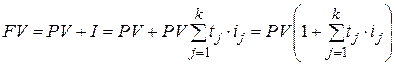| (2.37) |
При реинвестировании по простым процентным ставкам также может предусматриваться использование плавающих ставок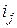 
. Тогда формула (2.10) примет вид:
 .
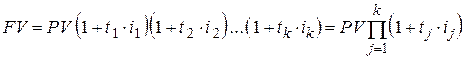| (2.38) |
Если условия ФО с наращением по сложной процентной ставке предусматривают использование плавающих ставок 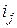, то за период времени, соответствующий продолжительности ФО и состоящий из k периодов, расчет наращенной суммы FV с учетом формулы (2.12) выполняют по формуле
|
|
|
 .
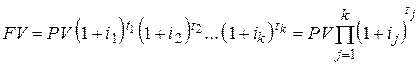| (2.39) |
Если плавающие ставки используются в ФО с наращением по простой учетной ставке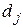 
, то для вывода формулы расчета наращенной суммы FV следует воспользоваться свойствами операции дисконтирования (см. раздел 5.4). При этом за каждый j -й период в соответствии с формулой (5.6) будет начислен дисконт 
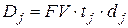, а за период времени, соответствующий продолжительности ФО и состоящий из k периодов, суммарный дисконт D составит
 .
|
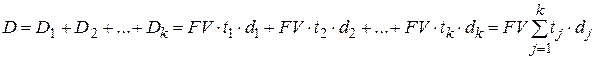Тогда по формуле (5.7) получим
 ,
|
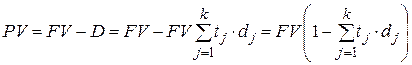откуда
 .
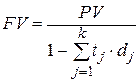| (2.40) |
Если плавающие ставки предусмотрены в ФО с наращением по сложной учетной ставке 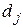, то по аналогии с формулами (2.39) и (2.40) получим следующую формулу для расчета расчет наращенной суммы FV:
 .
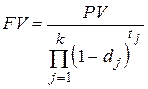| (2.41) |
Формулы (2.37), (2.39), (2.40) и (2.41) могут быть использованы в операциях дисконтирования, если их условиями предусмотрены плавающие ставки.
Пример 2.7. Финансовый кредит на сумму 50 000 рублей выдан на срок 2 года. В течение первого года ставка наращения составляет 15%, а каждые следующие полгода увеличивается на 2%. Определить наращенную сумму при использовании простой процентной ставки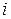 
и при реинвестировании.
