Уравнение Бернулли. Формула Торичелли

Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения (рис. 39). Рассмотрим объем жидкости, ограниченный стенками трубки тока и перпендикулярными к линиям тока сечениями S₁ и S₂. За время Δt этот объем переместится вдоль трубки тока, причем сечение S₁ переместится в положение S'₁, пройдя путь Δl₁, сечение S₂ переместится в положение S'₂, пройдя путь Δl ₂. В силу неразрывности струи заштрихованные объемы будут иметь одинаковую величину:
Δ V₁ =Δ V₂ = Δ V.

Энергия каждой частицы жидкости складывается из ее кинетической энергии и потенциальной энергии в поле сил земного тяготения. Вследствие стационарности те­чения частица, находящаяся спустя время Δt в любой из точек незаштрихованной части рассматриваемого объема (см., например, точку О на рис. 39), имеет такую же скорость (а следовательно, и кинетическую энергию), какую имела частица, находившаяся в той же точке в начальный момент времени. Поэтому приращение энергии ΔЕ всего рассматриваемого объема можно вычислить как разность энергий заштрихованных объемчиков Δ V₂ и Δ V₁.

Возьмем сечение трубки тока и отрезки Δl настолько малыми, чтобы всем точкам каждого из заштрихованных объемчиков можно было приписать одно и то же значение скорости v, давления р и высоты h. Тогда приращение энергии запишется следующим образом:

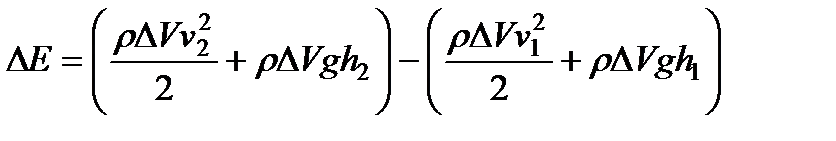(98)

(ρ – плотность жидкости).

В идеальной жидкости силы трения отсутствуют. Поэтому приращение энергии (98) должно равняться работе, совершаемой над выделенным объемом силами давления. Силы давления на боковую поверхность перпендикулярны в каждой точке к направлению перемещения частиц, к которым они приложены, вследствие чего работы не совершают. Отлична от нуля лишь работа сил, приложенных к сечениям S₁ и S₂. Эта работа равна

A = p₁S₁Δl₁ – p₂S₂Δl₂ = (p₁ – p₂)ΔV. (99)

Приравнивая выражения (98) и (99), сокращая на ΔV и перенося члены с одинаковыми индексами в одну часть равенства, получим:

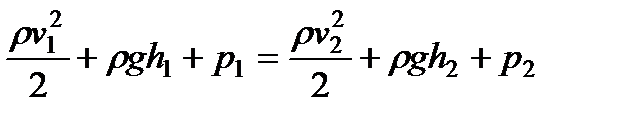. (100)

Сечения S₁ и S₂ были взяты совершенно произвольно. Поэтому можно утверждать, что в любом сечении трубки тока выражение 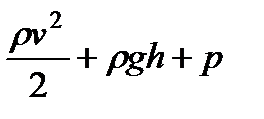имеет одинаковое значение. В соответствии со сделанными нами при его выводе предположениями уравнение (100) становится вполне точным лишь при стремлении поперечного сечения S к нулю, т. е. при стягивании трубки тока в линию. Таким образом, величины р, v и h, фигурирующие в левой и правой частях уравнения (100), следует рассматривать как относящиеся к двум произвольным точкам одной и той же линии тока.

Полученный нами результат можно сформулировать следующим образом: в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие

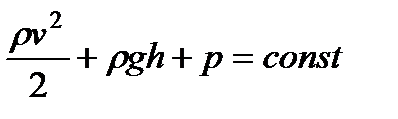(101)

Уравнение (101) или равнозначное ему уравнение (100) называется уравнением Бернулли. Несмотря на то, что это уравнение было получено нами для идеальной жидкости, оно достаточно хорошо выполняется для реальных жидкостей, внутреннее трение в которых не очень велико.

Рассмотрим некоторые следствия, вытекающие из уравнения Бернулли. Пусть жидкость течет так, что скорость имеет во всех точках одинаковую величину. Тогда согласно (100) для двух произвольных точек любой линии тока будет выполняться равенство

p₁ – p₂ = ρg(h₂ – h₁),

откуда следует, что распределение давления в этом случае будет таким же, как в покоящейся жидкости [см. (96)].

Для горизонтальной линии тока условие (100) принимает вид

,

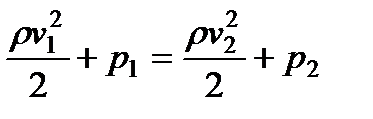т. е. давление оказывается меньшим в тех точках, где скорость больше (качественно это уже было показано в предыдущем параграфе).

Применим уравнение Бернулли к случаю истечения жидкости из небольшого отверстия в широком открытом сосуде. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность жидкости в сосуде, а с другой стороны — отверстие, через которое жидкость вытекает (рис. 40). В каждом из этих сечений скорость и высоту над некоторым исходным уровнем можно считать одинаковыми, вследствие чего к ним можно применить уравнение (100), полученное при этом предположении. Далее, давления в обоих сечениях равны атмосферному и поэтому одинаковы. Кроме того, скорость перемещения открытой поверхности в широком сосуде можно положить равной нулю. С учетом всего сказанного, уравнение (100) применительно к данному случаю можно написать в виде

,

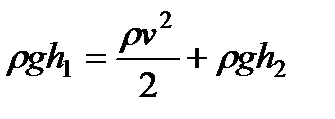где v — скорость истечения из отверстия. Сокращая на ρ и введя h = h₁ — h₂ — высоту открытой поверхности жидкости над отверстием, получаем:

,

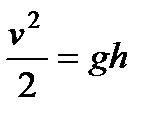Откуда

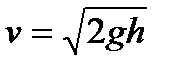. (102)

Эта формула называется формулой Торричелли.

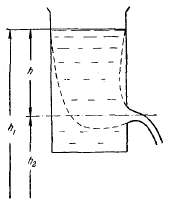
Рис. 40.

Истечение жидкости из отверстия

Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает любое тело, падая с высоты h.

Следует помнить, что этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения (102), чем больше вязкость жидкости.