Занятие 14. Средняя величина как обобщающая характеристика величин одного вида

1. Понятие средней величины

Большое распространение в статистике имеют средние величины. В средних величинах отображаются важнейшие показатели товарооборота, товарных запасов, цен. Средними величинами характеризуются качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.

Средняя величина имеет особое значение в условиях рыночной экономики, когда средняя через единичное и случайное позволяет выявить общее и необходимое, позволяет выявить тенденцию закономерностей экономического развития.

СРЕДНИЕ ВЕЛИЧИНЫ - это обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления.

При помощи средней величины происходит бы сглаживание различий в величине признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения. Например, средняя выработка продавца зависит от многих причин: квалификации, стажа, возраста, формы обслуживания и пр. Средняя выработка отражает свойство всей совокупности.

Средняя величина – величина абстрактная, потому что характеризует значение абстрактной единицы, а значит, отвлекается от структуры совокупности. Средняя характеризует то общее, что складывается в каждом отдельном, единичном объекте. Благодаря этому средняя получает большое значение для выявления закономерностей, присущих массовым общественным явлениям и не всегда заметных в единичных явлениях.

2. Виды средних величин

Имеется несколько видов средних величин, которые отличаются друг от друга способами исчисления.

Математическая статистика выводит различные средние из формулы степенной средней:

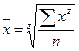
при z = 1 – средняя арифметическая;

при z = 0 – средняя геометрическая;

при z = -1 – средняя гармоническая;

при z = -2 – средняя квадратическая.

СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ - наиболее распространенный вид средней. Она исчисляется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.

ПРИМЕР:

Условия задачи: При обследовании предприятия, на котором работает 10 сотрудников, установлен их рабочий стаж: 6 лет, 5, 4, 3, 3, 4, 5, 4, 5, 4 года, т. е. дан ряд одиночных значений признака. Требуется вычислить средний стаж .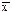

Решение 1: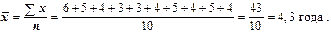

В данном случае средний стаж 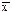рассчитывается как средняя арифметическая простая (невзвешенная) делением количества сводного признака на число показаний:

.

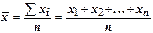Решение 2: Часто приходится рассчитывать среднее значение признака по ряду распределения, когда одно и то же значение признака встречается несколько раз. Объединив те же данные по величине признака (т. е. сгруппировав) и подсчитав число случаев повторения каждого из них, мы получим следующий вариационный ряд:

3, 3, 4, 4, 4, 4, 5, 5, 5, 6.

Это ряд распределения работающих на торговом предприятии по стажу работы.

Продолжительность стажа работы (варианты)	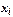Число работников торгового предприятия (частоты)	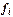Отработано человеко-лет	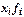Доля работников к общей численности работников (частости)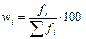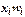
Итого:

Тогда средняя равна:

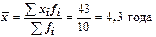
или как средняя арифметическая взвешенная:

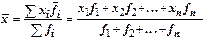
Следовательно, для исчисления взвешенной средней выполняются следующие последовательные операции:

1) умножение каждой варианты на её частоту,

2) суммирование полученных произведений,

3) деление полученной суммы на сумму частот.

В ряде случаев роль частот при исчислении средней играют какие-либо другие величины. Например, при исчислении средней урожайности единственно правильным будет взвешивание по размеру площади посева, а не по числу участков.

Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными величинами - частостями ( 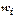). Заменив в этом примере абсолютные значения частот соответствующими относительными величинами, получим тот же результат:

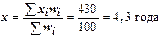
Средняя арифметическая взвешенная, следовательно, не какой-то особый вид средней, а такая средняя арифметическая, в которой сложение заменено умножением значений признака на их повторяемость (частоту) в случае, когда каждое значение повторяется в совокупности более чем один раз. Простая средняя арифметическая - частный случай средней арифметической взвешенной.

В некоторых случаях для расчета средней пользуются формулой средней гармонической.

СРЕДНЯЯ ГАРМОНИЧЕСКАЯ - это величина, обратная средней арифметической из обратных значений признака.

Простая средняя гармоническая рассчитывается по формуле:

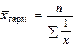
Средняя гармоническая взвешенная рассчитывается по следующей формуле:

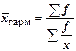
ПРИМЕР:

Условия задачи: Пусть имеются следующие данные об урожайности и валовом сборе пшеницы в 3-х колхозах (графы 2 и 3 табл.). Требуется определить среднюю урожайность пшеницы.

Фермерские хозяйства	Урожайность в ц с га	Валовый сбор пшеницы	Посевная площадь в га
Итого

Решение: Средняя урожайность может быть определена, если валовой сбор, полученный со всей площади, разделить на величину этой площади. В графе 4 рассмотренной таблицы приведены данные о посевных площадях каждого колхоза, рассчитанные путем деления валового урожая колхоза на его урожайность.

Для определения средней урожайности следует разделить итог графы 3 на итог графы 4:

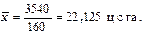
Запишем, как был получен этот результат из первоначальных данных, приведенных во 2-й и 3-й графах таблицы:

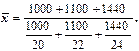
Считая, что графа вторая содержит индивидуальные значения признака, или, как их обычно обозначают, 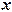, третья - веса, обычно обозначаемые 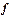, можем записать этот результат в виде следующей формулы:

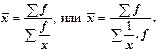
Итак, в данном случае для расчета средней урожайности была использована формула средней гармонической.

Отметим, что веса в данном случае не являлись частотами значений признака в совокупности, а представляли собой произведение самого значения признака на его частоту.

Отсюда можно сделать два вывода:

1) средняя гармоническая рассчитывается в тех случаях, когда располагают данными не о частотах различных значений признака, а об их произведениях на величину признака;

2) вместо средней гармонической всегда можно рассчитывать среднюю арифметическую, рассчитав предварительно на основе исходных данных частоты отдельных значений признака в совокупности.

3. Структурные средние величины

Для характеристики структуры совокупности применяются особые показатели, которые можно назвать структурными средними. К таким показателям относятся мода и медиана.

МОДОЙ (Мо) называется чаще всего встречающийся вариант, или модой называется то значение признака, которое соответствует максимальной точке теоретической кривой распределения.

Мода представляет наиболее часто встречающееся или типичное значение. Мода широко используется в коммерческой практике при изучении покупательского спроса (при определении размеров одежды и обуви, которые пользуются широким спросом), регистрации цен. В дискретном ряду мода - это вариант с наибольшей частотой. Например, по приведенным ниже данным наибольшим спросом обуви пользуется размер 37:

Размер обуви	Число купленных пар
	88 (Мо )

В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту (частость). В пределах интервала надо найти то значение признака, которое является модой. Решение вопроса состоит в том, чтобы в качестве моды выявить середину модального интервала. Такое решение будет правильным лишь в случае полной симметричности распределения либо тогда, когда интервалы, соседние с модальными, мало отличаются друг от друга по числу случаев. В противном случае середина модального интервала не может рассматриваться, как мода. Конкретное значение моды для интервального ряда определяется формулой:

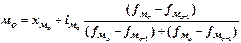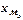; где - нижняя граница модального интервала; 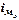- величина модального интервала; 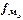- частота, соответствующая модальному интервалу; 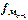- частота, предшествующая модальному интервалу; 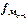- частота интервала, следующего за модальным. Эта формула основана на предположении, что расстояния от нижней границы модального интервала до моды и от моды до верхней границы модального интервала прямо пропорциональны разностям между численностями модального интервала и прилегающих к нему.

ПРИМЕР: Дан интервальный ряд, характеризующий стаж сотрудников предприятия. Найти модальный интервал и моду.

Стаж (лет)	Число работников
До 2
2-4
4-6
6-8
8-10
Свыше 10

Решение: В нашем примере модальным интервалом величины стажа работников торгового предприятия будут 6 - 8 лет, а модой продолжительности стажа - 6,77 года:

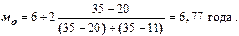
Мода всегда бывает несколько неопределенной, так как она зависит от величины групп, от точного положения границ групп.

МЕДИАНА (Ме)-это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая - большие.

Понятие медианы легко уяснить из следующего примера. Для ранжированного ряда (т. е. построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом членов медианой является варианта, расположенная в центре ряда.

ПРИМЕР: В ранжированных данных о стаже работы семи продавцов - 1, 2, 2, 3, 5, 7, 10 лет - медианой является четвертая варианта - 3 года. Для ранжированного ряда с четным числом членов (индивидуальных величин) медианой будет средняя арифметическая из двух смежных вариант. Если в бригаде продавцов из шести человек распределение по стажу работы было таким: 1, 3, 4, 5, 7, 9 лет, то медианой будет значение, равное: (4+5): 2= 4,5 года, т.е.

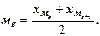
В интервальном вариационном ряду порядок нахождения медианы следующий:

1) располагаем индивидуальные значения признака по ранжиру;

2) определяем для данного ранжированного ряда накопленные частоты;

3) по данным о накопленных частотах находим медианный интервал;

4) медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.

Если предполагать, что внутри медианного интервала нарастание или убывание изучаемого признака происходит по прямой равномерно, то формула медианы в интервальном ряду распределения будет иметь следующий вид:

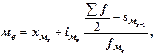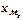где - нижняя граница медианного интервала; 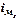- величина медианного интервала; 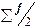- полусумма частот ряда; 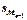- сумма накопленных частот, предшествующих медианному интервалу; 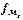- частота медианного интервала.

Медиана ряда наблюдений может быть очень далека от его типичной величины и в действительности может не приближаться ни к одному из наблюдаемых объектов. Но поскольку медиана является серединным (центральным) значением, это делает ее смысл вполне ясным. Медиана по своему положению более определенна, чем мода.

Медиана находит практическое применение вследствие особого свойства - сумма абсолютных отклонений членов ряда от медианы есть величина наименьшая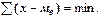

ПРИМЕР:

Условия задачи: В таблице, графа 2, приведена удаленность магазинов от центральной базы. Определить отклонения от среднего арифметического значения (графа 3) и от медианного значения (графа 4).

Решение: Определим среднее арифметическое - 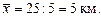Определим отклонение от среднего арифметического для каждого случая по формуле: 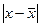, значение помещаем в графу 3.

Значение медианы получаем из 2 графы, ряд нечетный, Ме =4 км. Аналогично получаем значения отклонения от медианы, результат – в графе 4.

№ п/п	Расположение магазинов от базы снабжения, км	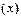Отклонения от среднего значения	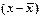Отклонения от медианного значения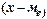
Итого

Вышеназванное свойство Ме находит широкое практическое применение в маркетинговой деятельности.

Величины, приходящиеся на одной четверти и на трех четвертях расстояния от начала ряда, называются квартилями, на одной десятой - децилями, на одной сотой - процентилями.

При статистическом изучении совокупности правильно выбранная средняя обладает следующими свойствами:

1) Если в индивидуальном признаке явления есть какая-либо типичность, то средняя ее обнаруживает, но она учитывает и влияние крайних значений.

2) Если 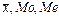совпадают, то данная группа симметрична. Но

3) 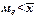при немногочисленной группе с очень высокими числами и 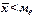, если нет очень больших чисел и данные концентрируются.

4) Если совокупность неоднородна, то мода трудно определяется.

5) 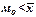, если имеется немногочисленная группа с высокими числами и 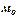отчетливо выражена при однородности группы.

...