Графическое изображение термодинамических процессов

Уравнение Менделеева — Клапейрона 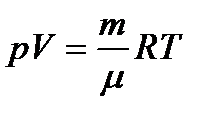устанавливает связь между тремя основными параметрами р, V и Т, характеризующими данную массу газа. Таким образом, из трех параметров любые два могут рассматриваться как независимые, а третий может быть выражен через них. Выбирая в качестве независимых параметров, определяющих состояние газа, р и V, можно записать температуру в виде

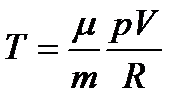. (94)

Это позволяет наглядно изображать с помощью графиков состояние газа и происходящие в нем процессы.

Будем откладывать значения объема газа V на оси абсцисс, а значения давления р — на оси ординат (рис. 35). Каждому состоянию газа, характеризуемому определенными значениями V и р, отвечает на этом графике точка с координатами (V, р). И обратно, точка I на этом графике изображает состояние газа со значениями объема V = V₁ и давления р = p₁. Соответствующая этому состоянию температура Т = Т₁ определится по уравнению (94).

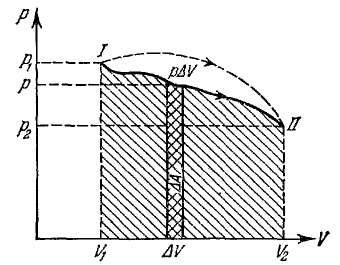
Рис. 35. pV-диаграмма термодинамического процесса

При изменении состояния газа величины р и V (и связанная с ними температура Т) будут непрерывно меняться, а изображающая состояния точка в pV-диаграмме будет перемещаться вдоль некоторой кривой. Сплошная кривая между точками I и II полностью отражает произведенный процесс изменения состояния газа.

С помощью pV-диаграммылегко вычислить работу, совершенную газом при данном процессе. Рассмотрим достаточно малый интервал изменения состояния, когда объем газа изменяется от произвольного значения V до значения V + ΔV. При малом изменении объема ΔV давление можно считать практически постоянным иравным р. Согласно (78) элементарная работа, совершенная газом при расширении на величину ΔV, равна

A = p ΔV. (95)

Из рис. 35 видно, что величина ΔAчисленно равна площади полоски, заштрихованной на этом графике двойной штриховкой. Разбивая полное изменение объема от V₁ до V₂ на ряд последовательных приращений ΔV, мы найдем полную работу, совершенную газом в течение данного процесса, как сумму площадей таких полосок:

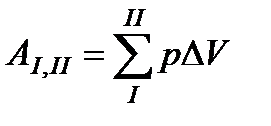(96)

В пределе эта работа изобразится полной площадью, заключенной между кривой, изображающей процесс, осью абсцисс и двумя ординатами, восставленными в конечных точках V₁ и V₂. Эта площадь на рис. 35 показана простой штриховкой.

Условие постоянства давления р при малом изменении объема ΔV будет соблюдаться тем лучше, чем меньше величина ΔV, что хорошо видно из графика. Значение искомой работы А_I,II будет вычислено тем точней, чем меньше Δ V, т. е. чем больше полосок помещается между V₁ и V₂. Точное значение А_I,II мы получим, переходя к пределу бесконечно большого числа бесконечно тонких полосок. Такая сумма записывается символически в виде определенного интеграла:

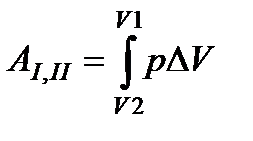(97)

Если мы переведем газ из того же начального состояния (V₁, p₁) в то же конечное состояние (V ₂, р₂) через другой ряд промежуточных состояний, то этот новый процесс в pV -диаграмме изобразится другой линией, соединяющей те же точки I и II. На рис. 35 такой процесс изображен пунктирной линией.

Как видно из рисунка, площадь, ограниченная сверху пунктирной кривой и численно равная работе А’_I,II, при втором процессе отличается от площади, ограниченной первой кривой. Таким образом, работа, совершаемая газом при изменении его состояния, зависит не только от его начального и конечного состояний, но и от пути перехода из одного в другое. Переводя газ из состояния I в состояние II, можно получить самую различную работу, в зависимости от способа («пути») перехода.

Этот вывод нисколько не противоречит закону сохранения энергии — первому началу термодинамики, — поскольку при различных процессах газ не только совершает различную механическую работу, но и получает от окружающих тел различные количества теплоты. Для пояснения этого обстоятельства разберем детальнее несколько простейших процессов с газами, представляющих также и технический интерес.

Термодинамические процессы, происходящие в системе с постоянной массой при каком-либо одном постоянном параметре, называются изопроцессами.