Пусть нагревание происходит в условиях, когда объем остается постоянным (V = const). Соответствующая молярная теплоемкость называется теплоемкостью при постоянном объеме, или изохорической теплоемкостью, и обозначается CV:
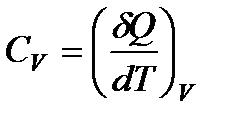 (82)
(82)
Так как теплота при этом тратится только на изменение внутренней энергии dU, то δ Q = dU и
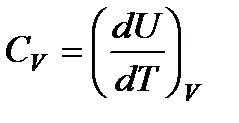 (83)
(83)
Отсюда dU = CV dT. Уравнение закона сохранения энергии (80) можно теперь переписать в виде
δQ = CVdT + pdV. (84)
Следовательно, подводимое к телу тепло расходуется на изменение температуры dT (изменение внутренней энергии) и изменение объема dV (с этим связана внешняя механическая работа).
Если при нагревании постоянным остается давление, то теплоемкость называется теплоемкостью при постоянном давлении Ср (ее можно также называть изобарической теплоемкостью):


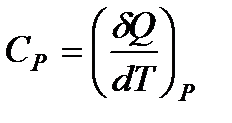 .
.
Пользуясь результатами кинетической теории газов, легко вычислить молярные теплоемкости идеального газа.
Для идеального одноатомного газа, как мы видели, внутренняя энергия моля равна U = 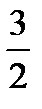 RT; значит,
RT; значит,
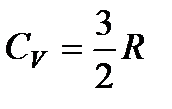 . (85)
. (85)
Если разделить это значение молярной теплоемкости на число молекул в грамм-молекуле, т. е на число Авогадро, то получим тот средний вклад, который каждая молекула вносит в теплоемкость газа:
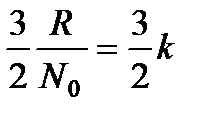 .
.
Следовательно, при повышении температуры на 1 К энергия каждой молекулы в среднем возрастает на 
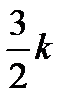 джоулей.
джоулей.
Теплоемкость Cp идеального газа при постоянном давлении больше теплоемкости CV при постоянном объеме на величину работы, которую совершает моль газа, расширяясь при нагревании на 1К. Работа эта равна 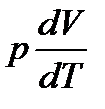 . Таким образом,
. Таким образом,
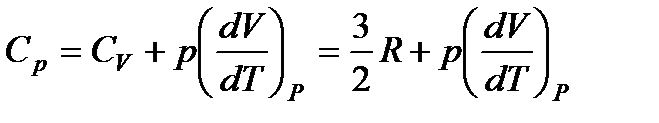 . (86)
. (86)
Но для моля идеального газа pV = RT, поэтому 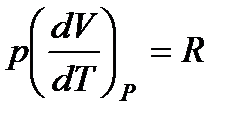 и
и
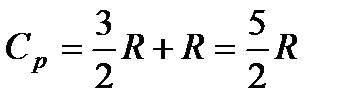 . (87)
. (87)
Из формул (85) и (87) видно, что теплоемкость при постоянном давлении превосходит теплоемкость при постоянном объеме на величину R:
CP – CV = R. (88)
Уравнение (88) называется уравнением Роберта Майера. Из него вытекает физический смысл газовой постоянной:
 2015-02-15
2015-02-15 18954
18954
